Particule sur un segment - position la plus probable
Durée : 10 mn
Note maximale : 5
Question
Soit\(\Psi_{\textrm{n}}\textrm{(x,t)}\)une fonction d'onde stationnaire et normalisée décrivant un état quantique d'une particule astreinte à se déplacer sur un axe x'Ox entre deux bornes \(\textrm{X} = 0\) et \(\textrm{X} = \textrm{L}\). On ne travaille que sur la partie spatiale de la fonction d'onde que l'on prend sous la forme suivante :
\(\mathrm{\Psi_{n}(x) = \sqrt{ \frac{2}{L}} \sin (n \pi x/L )}\)
où n un entier strictement positif.
La position la plus probable correspond à l'endroit où la densité de probabilité de présence est maximale.
Déterminer les positions les plus probables dans les états\(\Psi_{\textrm{n}}\textrm{(x)}\).
Application aux états \(\Psi_{\textrm{1}}\textrm{(x)}\)et\(\Psi_{\textrm{2}}\textrm{(x)}\).
On donne : \(\mathrm{2 \sin^{2} (u) = 1 - \cos(2u)}\)
Solution
On exprime la densité et on cherche son maximum.
La densité de probabilité de présence est égale au carré du module de la fonction d'onde.
On a donc :
\(\mathrm{\mid \Psi_{n}(x)\mid^{2} = \frac{2}{L} \sin^2 (n\pi x/L)}\)
Il suffit de chercher un extremum entre 0 et L. On cherche donc à annuler la dérivée de la densité.
\(\mathrm{\frac{d}{dx}\big[\mid\Psi_{n}(x)\mid^{2}\big] = \frac{2}{L}\frac{d}{dx}\big[\sin^2 (n\pi x/L)\big] = - \frac{1}{L}\frac{d}{dx}[\cos(2n\pi x/L)]}\)
\(\mathrm{\frac{d}{dx}\big[\mid\Psi_{n}(x)\mid^{2}\big] = + \frac{2n\pi}{L}\sin(2n\pi x/L) = 0}\)
Cette dérivée s'annule lorsque
\(\mathrm{\sin (n\pi x/L) = 0}\)
\(\mathrm{\frac{n\pi x}{L} = k\pi}\) et \(\mathrm{x = \frac{Lk}{n}}\)
La particule est sur le segment de longueur L ; on doit donc ne retenir que les positions comprises entre 0 et L. Par exemple pour n=1, on retient la solution \(\textrm{x} = \frac{\textrm{L}}{2}\). La position la plus probable est au milieu du segment. Pour n=2, il y a trois valeurs possibles : x = L/4, L/2 et 3L/4. La densité étant nulle en L/2, cette position ne peut être qu'un minimum.
Densité de probabilité de présence dans les états \(\Psi_{1}\textrm{(x)}\)et\(\Psi_{2}\textrm{(x)}\)
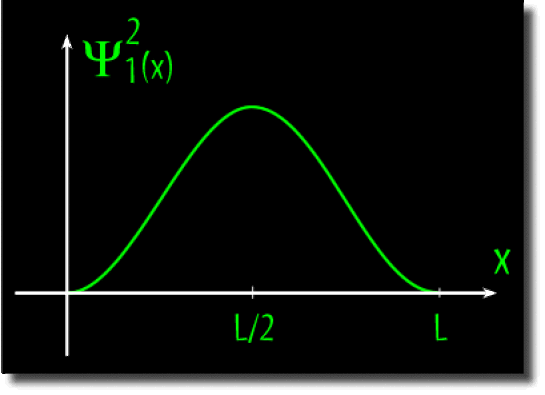
Son maximum est en L/2.
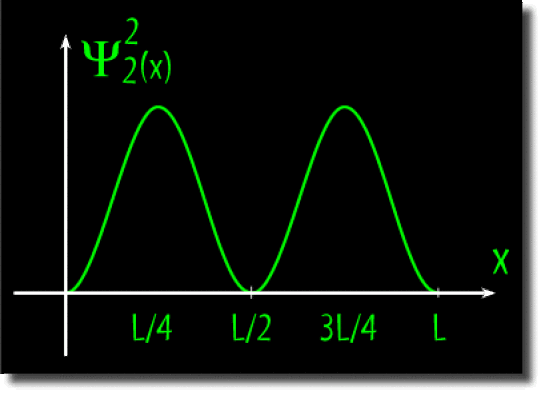
Ses maxima équiprobables sont en L/4 et 3L/4.