Probabilité de présence de l'électron dans un volume fini
Partie
Question
La densité radiale de probabilité de présence dans l'état quantique\(\mathrm{1s}\) d'un atome ou ion hydrogénoïde est :
\(\mathrm{D(r)}=4\pi~\mathrm{r}^2\psi^2=4\mathrm{r}^2\left(\frac{\textrm{Z}}{a_0}\right)^3 \exp\left(-\frac{2~\textrm{Zr}}{a_0}\right)\)
- Exprimer la probabilité de présence à l'intérieur d'une sphère de rayon\( \mathrm{R}\).
- Tracer la courbe \(\mathrm{P(R)}\) pour \(\mathrm{H}\), \(\mathrm{He}^+\) et \(\mathrm{Li}^{2+}\).
- Interpréter ces trois courbes pour estimer les tailles relatives des trois atomes.
Aide simple
On donne la formule d'intégration suivante :
\(\int_{r=0}^{R}\exp~(-2\textrm{Ar})~\mathrm{dr=-\frac{1}{2\mathrm{A}}}\left[\exp~(-2\mathrm{Ar})\right]_0^{\mathrm{R}}\)
Aide méthodologique
Il faut procéder à l'intégration de la densité radiale entre \(\mathrm{r}=0\) et \(\mathrm{r=R}\).
On rappelle la règle suivante pour les intégrations par partie :
\((\textrm{UV})~'=\textrm{UV}~'+\textrm{U}~'\textrm{V}\)
Il faut proposer un critère de taille pour l'atome, basé sur la courbe \(\mathrm{P(R)}.\)
Aide à la lecture
La densité radiale de probabilité de présence permet de déterminer la contribution de la sphère de rayon\( \mathrm{r}\) à la probabilité de présence. La probabilité demandée fait la somme des densités de toutes les sphères de rayon \(\mathrm{r}<\mathrm{R}\).
Solution détaillée
La probabilité de présence élémentaire dans une couche sphérique d'épaisseur \(\mathrm{dr}\) et de rayon \(\mathrm{r}\) est donnée par :
\(\mathrm{dP_r}=\mathrm{D(r)~dr}=4\mathrm{r}^2~\left(\frac{\mathrm{Z}}{\mathrm{a_0}}\right)^3\exp\left(-\frac{2~\mathrm{Zr}}{\mathrm{a_0}}\right)~\mathrm{dr}\)
La probabilité de présence à l'intérieur d'une couche de rayon \(\mathrm{R}\) est obtenue en intégrant entre \(\mathrm{r=0}\) et \(\mathrm{r=R}\).
\(\mathrm{P(R)}=\int_\mathrm{r=0}^\mathrm{R}\mathrm{dP_r}=4~\left(\frac{\mathrm{Z}}{\mathrm{a_0}}\right)^3\int_\mathrm{r=0}^\mathrm{R}\mathrm{r}^2\exp\left(-\frac{2~\mathrm{Zr}}{\mathrm{a_0}}\right)\mathrm{dr}\)
On pose \(\mathrm{A}=\frac{Z}{a_0}\)pour simplifier l'écriture.
\(\mathrm{P(R)}=4\mathrm{A}^3\int_{\mathrm{r=0}}^{\mathrm{R}}\mathrm{r}^2\exp~(-2\mathrm{Ar})~\mathrm{dr}\)
Il faut procéder à une double intégration par parties.
\(\mathrm{P(R)}=4\mathrm{A}^3\left(~\left[-\frac{1}{2\mathrm{A}}\mathrm{r}^2\exp~(-2\mathrm{Ar})\right]_0^R+\frac{1}{\mathrm{A}}\int_\mathrm{r=0}^\mathrm{R}\mathrm{r}~\exp~(-2\mathrm{Ar})~\mathrm{dr}~\right)\)
\(\mathrm{P(R)}=4\mathrm{A}^3\left(-\frac{\mathrm{R}^2}{2\mathrm{A}}\exp~(-2\mathrm{AR})~+\frac{1}{\mathrm{A}}\int_\mathrm{r=0}^{R}\mathrm{r}\exp~(-2\mathrm{Ar})~\mathrm{dr}\right)\)
\(\mathrm{P(R)}=4\mathrm{A}^3\left(-\frac{\mathrm{R}^2}{2\mathrm{A}}\exp~(-2\mathrm{AR})~+\frac{1}{\mathrm{A}}\left[-\frac{1}{2\textrm{A}}\mathrm{r}~\exp~(-2\mathrm{Ar})\right]_0^\mathrm{R}+\frac{1}{2\mathrm{A}^2}\int_\mathrm{r=0}^\mathrm{R}\exp~(-2\mathrm{Ar})~\mathrm{dr}\right)\)
\(\mathrm{P(R)}=4\mathrm{A}^3\left(-\frac{\mathrm{R}^2}{2\mathrm{A}}\exp~(-2\mathrm{AR})-\frac{\mathrm{R}}{2\mathrm{A}^2}\exp~(-2\mathrm{AR})-\frac{1}{4\mathrm{A}^3}\exp~(-2\mathrm{AR})+\frac{1}{4\mathrm{A}^3}\right)\)
On obtient en définitive :
\(\mathrm{P(R)}=1-\exp~(-2\mathrm{AR})(1+2\mathrm{AR}+2\mathrm{A}^2\mathrm{R}^2)\)
soit :
\(\mathrm{P(R)}=1-\exp\left(-2\frac{\mathrm{ZR}}{\mathrm{a_0}}\right)\left[1+2\frac{ZR}{\mathrm{a_0}}+2\left(\frac{\mathrm{ZR}}{\mathrm{a_0}}\right)^2\right]\)
La figure suivante donne l'allure de\( \mathrm{P(R)}\) pour l'hydrogène \(\mathrm{(Z = 1})\) et les cations \(\mathrm{He}^+\) \(\mathrm{(Z = 2)}\)
et \(\mathrm{Li}^2+\) \(\mathrm{(Z = 3)}\).
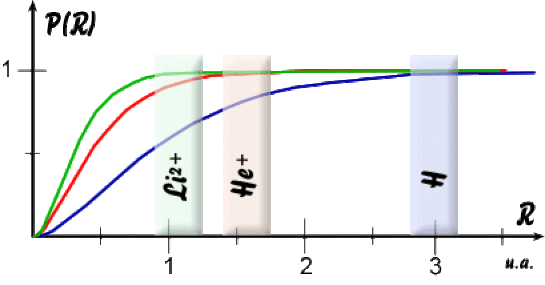
La probabilité de présence augmente quand la taille de la sphère augmente. Elle tend vers une asymptote correspondant à une probabilité certaine \(\mathrm{(P = 1)}\) : la portion des courbes qui rejoint l'asymptote donne une estimation de la taille du nuage électronique. Quand on atteint cette zone, on peut considérer que l'on a sondé l'essentiel du nuage électronique représentant l'électron.
La comparaison des trois courbes permet d'estimer la taille relative des atomes. On atteint l'asymptote pour des valeurs de \(\mathrm{R}\) d'autant plus petites que \(\mathrm{Z}\) est grand. Les nuages électroniques \(\mathrm{1s}\) de \(\mathrm{Li}^{2+}\), \(\mathrm{He}^+\)+ et \(\mathrm{H}\) ont donc des extensions croissantes. Ceci traduit la diminution de l'attraction par le noyau dont la charge passe de \(\mathrm{+3e}\) à \(\mathrm{+e.}\)