Structure de l'aluminium
Partie
Question
La maille de l'aluminium est-elle de type cubique centré ou cubique à faces centrées ?
Déterminer le paramètre de maille.
On donne :
Masse volumique de l'aluminium : \(\mathrm{2,7 ~g.cm^{-3}}\)
Rayon atomique : \(1,43~\AA\)
Masse molaire : \(27~\mathrm{g.mol^{-1}}\)
Nombre d'Avogadro :\( \mathrm{N = 6,02~.10^{23}~mol^{-1}}\)
Aide simple
Identifier les directions selon lesquelles les atomes sont tangents pour relier le paramètre de maille et le rayon atomique.
Aide méthodologique
Représenter la maille dans les deux cas de figure.
Déterminer le nombre de groupements formulaires Z, le paramètre de maille et la masse volumique.
La comparaison avec les données permet alors de trancher.
Aide à la lecture
Il faut pouvoir trancher entre les deux possibilités à partir des données fournies.
Solution détaillée
Considérons le système cubique centré. On a représenté la maille ci-dessous. Les atomes sont tangents selon la grande diagonale du cube de longueur \(\mathrm{a\sqrt3}\).
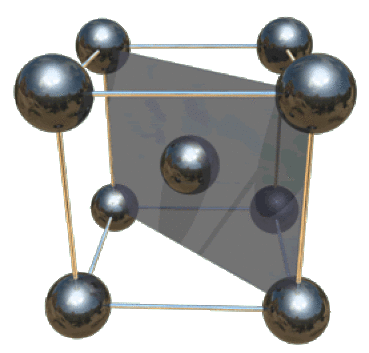
On a : \(\mathrm{a\sqrt3=4R}\) soit \(\mathrm{a=4\frac{R}{\sqrt3}=\frac{4\times1,43}{\sqrt3}=3,30~\AA}\).
Le nombre de groupements formulaires dans une maille cubique centrée est :
\(\mathrm{Z=8\times\frac{1}{8}+1\times1=2}\)
La masse volumique est le rapport de la masse des atomes sur le volume de la maille. On ramène tout à une mole de mailles :
\(\rho=\mathrm{\frac{ZM}{NV}=\frac{2\times27}{6,02.10^{23}\times\left(3,30.10^{-8}\right)^3}=2,49~g.cm^{-3}}\)
Ce n'est pas la valeur mesurée. L'aluminium doit donc être de type cfc.
On vérifie que l'on retrouve bien la valeur mesurée dans ce cas.
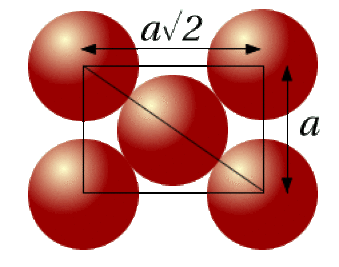
On a représenté la maille cfc ci-dessous. Les atomes sont tangents selon la diagonale d'une face du cube, de longueur \(\mathrm{a\sqrt2}\).
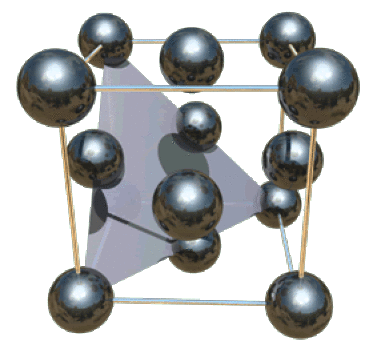
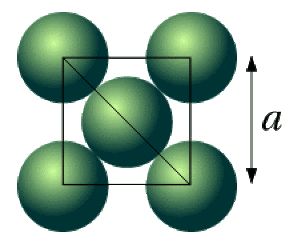
On a :\(\mathrm{a\sqrt2=4R}\) soit \(\mathrm{a=4\frac{R}{\sqrt2}=\frac{4\times1,43}{\sqrt2}=4,04\AA}\).
Le nombre de groupements formulaires dans une maille cubique à faces centrées est :
\(\mathrm{Z=8\times\frac{1}{8}+6\times\frac{1}{2}=4}\)
La masse volumique est alors :
\(\rho=\mathrm{\frac{ZM}{NV}=\frac{4\times27}{6,02.10^{23}\times\left(4,04.10^{-8}\right)^3}=2,72~g.cm^{-3}}\)
C'est bien le résultat mesuré. L'aluminium cristallise dans le système cfc.