Structure de l'alliage or-cuivre
Partie
Question
Le cuivre cristallise dans le système cfc avec un paramètre de maille \(\mathrm{a}=3,61\AA\).
L'or cristallise aussi dans le système cfc avec un paramètre de maille\(\mathrm{a}=4,08\AA\) .
L'alliage or-cuivre cristallise dans le système cubique simple, les atomes d'or occupent les sommets du cube et les atomes de cuivre le centre des faces.
Dessiner la maille de l'alliage, en déduire sa formule et calculer le paramètre de maille.
Calculer la masse volumique de l'alliage.
On donne :
Masse molaire de l'or : \(196,97~\mathrm{g.mol^{-1}}\)
Masse molaire du cuivre :\( 63,54~\mathrm{g.mol^{-1}}\)
Nombre d'Avogadro : \(\mathrm{N} = 6,02.10^{23}\mathrm{mol}^{-1}\)
Aide simple
Identifier les directions selon lesquelles les atomes sont tangents pour relier le paramètre de maille et les rayons atomiques.
On rappelle la formule de la masse volumique :
\(\rho=\mathrm{\frac{ZM}{NV}}\)
où V est le volume de la maille (en \(\mathrm{cm^3}\)) et M est la masse molaire du groupement formulaire (en \(\mathrm{g.mol^{-1}}\)).
Aide méthodologique
On utilisera les données de l'énoncé pour trouver les rayons atomiques nécessaires à la résolution du problème.
Aide à la lecture
Il faut exprimer le paramètre de maille en fonction du réseau et de la nature des atomes qui le composent.
Solution détaillée
On a représenté la maille ci-dessous. Les atomes sont tangents selon la grande diagonale du cube de longueur \(\mathrm{a\sqrt3}\)
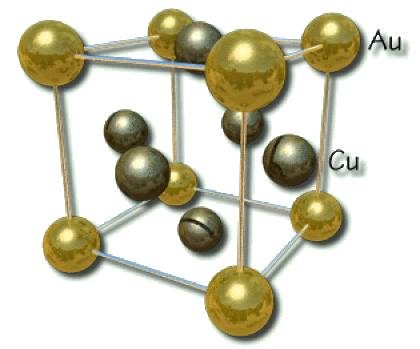
On calcule le nombre d'atomes dans la maille.
Au : un atome à chaque sommet : \(8\times\frac{1}{8}=1\)
Cu : un atome au centre de chaque face : \(6\times\frac{1}{2}=3\)
La composition de cet alliage est \(\mathrm{Cu_3Au}\).
Pour calculer le paramètre de maille, on représente une face du cube sur laquelle les atomes sont tangents :
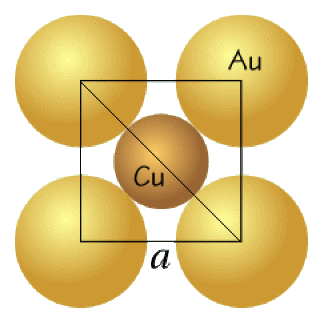
On a : \(\mathrm{a\sqrt2=2R_{Au}~+2R_{Cu}}\)
Les rayons atomiques sont obtenus dans les cristaux purs de cuivre et d'or. Ils cristallisent tous deux sous la forme cfc. On a donc :
\(\mathrm{a_{Au}\sqrt2=4R_{Au}}\) et \(\mathrm{a_{Cu}\sqrt2=4R_{Cu}}\)
soit :
\(\mathrm{R_{Au}=\frac{\sqrt2}{4}a_{Au}=1,44\AA}\) et \(\mathrm{R_{Cu}=\frac{\sqrt2}{4}a_{Cu}=1,28\AA}\)
Il vient en définitive :
\(\mathrm{a=\frac{2R_{Au}+2R_{Cu}}{\sqrt2}}=2\times\frac{1,28+1,44}{\sqrt2}=3,85\AA\)
Dans un système cubique simple, il y a un seul groupement formulaire : Z = 1.
La masse molaire de\( \mathrm{Cu_3Au}\) est :
\(\mathrm{M=3\times63,54+196,97=387,59~g.mol^{-1}}\)
La masse volumique est alors :
\(\rho=\mathrm{\frac{ZM}{NV}=\frac{1\times387,59}{6,02.10^{23}\times\left(3,85.10^{-8}\right)^3}=11,28~g.cm^{-3}}\)