Structure d'ordre
Définition : Minoration, majoration
Soient \(f\) et \(g\) deux fonctions définies sur \(I\); on dit que \(g\) majore \(f\), ou que \(f\) minore \(g\), si l'on a, pour tout \(x\in I, f(x)\leq g(x)\).
On note \(f\leq g\).
On vérifie immédiatement qu'il s'agit d'une relation d'ordre sur \(F(I, \mathbb R)\) et que cette relation d'ordre n'est pas totale. Deux fonctions quelconques ne sont pas en général comparables.
Exemple :
Exemple 1 :
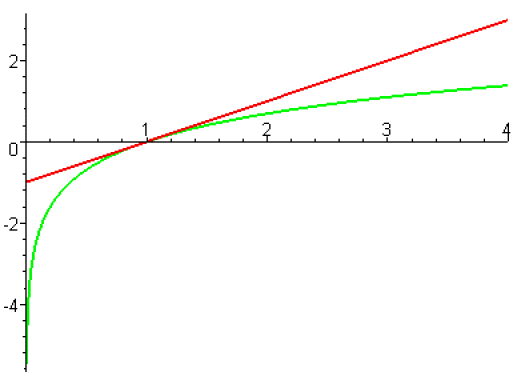
Sur l'intervalle \(]0,+\infty[\) la fonction \(x\mapsto x-1\) majore la fonction logarithme.
Exemple 2 :
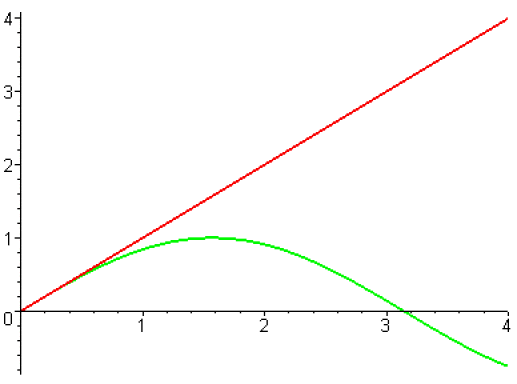
Sur l'intervalle \([0,+\infty[\) la fonction \(x \mapsto\sin x\) est majorée par la fonction \(x\mapsto x\).
Exemple 3 :
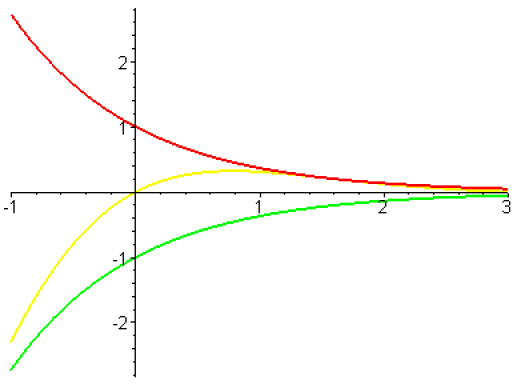
Sur \(\mathbb R\), la fonction \(x\mapsto\textrm e^{-x}\sin x\) est majorée par la fonction \(x\mapsto\textrm e^{-x}\) et minorée par la fonction \(x\mapsto-\textrm e^{-x}\) .