Cas où l'exposant est un entier strictement positif
Soit \(f\) la fonction \(x \mapsto x^n\) pour \(n \in \mathbb N ^*.\)
Cette fonction est le produit de \(n\) fonctions \(x \mapsto x,\) elle est continue et dérivable sur \(\mathbb R.\)
Sa dérivée est la fonction \(f' : x \mapsto nx^{n - 1}\)pour \(n \geq 2,~\textrm{et}~x \mapsto 1\) dans le cas \(n = 1.\) Elle est positive sur \(\mathbb R ^+\) pour tout \(n.\)
Lorsque \(n\) est pair, on a : \(\forall x \in \mathbb R~~(-x)^n = x^n.\) La fonction \(f\) est donc paire.
Lorsque \(n\) est impair, on a : \(\forall x \in \mathbb R~~(-x)^n = -x^n.\) La fonction \(f\) est donc impaire.
Pour tout entier \(n\) strictement positif, on a : \(\displaystyle \lim_{x \rightarrow +\infty}x^n = +\infty.\)
Démonstration :
Il s'agit de démontrer que : \(\forall A > 0, \exists B > 0~~|~~\forall x \in \mathbb R~~x > B \Rightarrow x^n > A.\)
On cherche donc une condition suffisante pour que \(x^n > A.\)
On sait que pour tout entier \(n\) strictement positif, on a \(\forall x \in \mathbb R, x >1 \Rightarrow x^n \geq x.\)
Pour que \(x^n > A,\) il suffit donc que l'on ait \(x > 1~\textrm{et}~x>A ,\) c'est-à-dire \(x > max(1, A).\)
On peut choisir \(B = max(1, A).\)
En effet, si \(x > B,\) alors \(x > 1~\textrm{et}~x > A,\) donc \(x^n \geq x~\textrm{et}~x > A, ~\textrm{d'où}~ x^n > A.\)
Et, suivant la parité de \(n\) :
si \(n\) est pair \(\displaystyle \lim_{x \rightarrow -\infty}x^n = +\infty\)
si \(n\) est impair \(\displaystyle \lim_{x \rightarrow -\infty}x^n = -\infty\)
D'où les tableaux de variations selon la parité de \(n\) :
Cas où \(n\) est pair
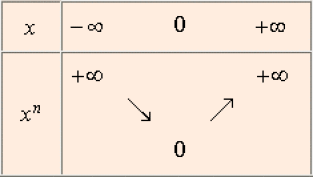
Cas où \(n\) est impair
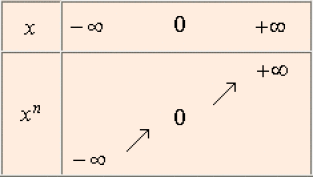
Voici, dans un repère orthogonal, quelques exemples de graphes :
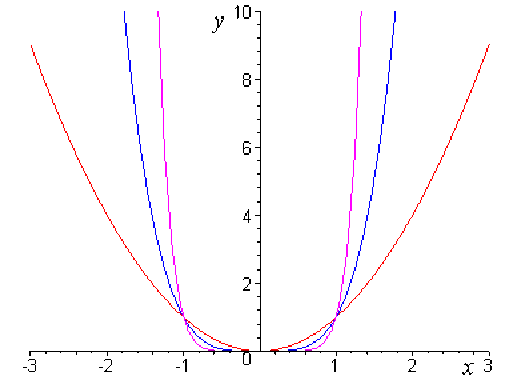
Cas où \(n\) est pair :
\(\color{red} x \mapsto x^2\)
\(\color{blue} x \mapsto x^4\)
\(\color{magenta} x \mapsto x^8\)
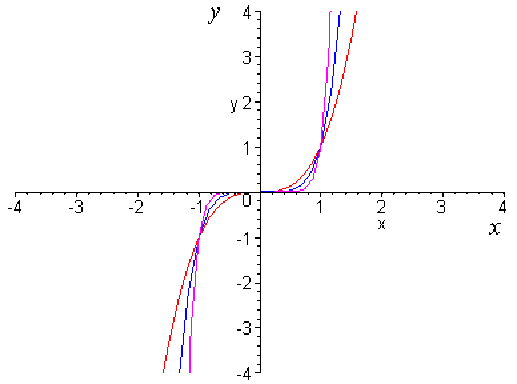
Cas où \(n\) est impair :
\(\color{red} x \mapsto x^3\)
\(\color{blue} x \mapsto x^5\)
\(\color{magenta} x \mapsto x^9\)
Remarque :
Pour plus de lisibilité, les repères ont été choisis orthogonaux, mais non orthonormés.