Polynômes de matrices
Partie
Question
Soit la matrice, à coefficients réels, \(A=\left(\begin{array}{cc}1&-1\\2&5\end{array}\right)\).
Déterminer le polynôme caractéristique de \(A\).
En utilisant la division euclidienne du polynôme \(P(X)=2X^4-12X^3+19X^2-29X+37\) par le polynôme caractéristique de \(A\), montrer qu'il existe des réels \(\alpha\) et \(\beta\) tels que la matrice \(P(A)\) soit égale à la matrice \(\alpha A+\beta I_2\) (préciser les valeurs de \(\alpha\) et \(\beta\)).
En déduire que la matrice \(P(A)\) est inversible et écrire son inverse sous la forme \(T(A)\), avec \(T(X)=\lambda X+\mu\) (\(\lambda\) et \(\mu\) étant des réels à calculer).
Aide simple
\(P_{\textrm{car},A}(X)=\textrm{det }(A-XI_2)\).
Rappel du théorème de Cayley-Hamilton : \(P_{\textrm{car},A}(A)=0\).
Une matrice est inversible si et seulement si son déterminant n'est pas nul.
Utiliser l'expression \(\alpha A+\beta I_2\) de \(P(A)\).
Exprimer \(A^2\) comme combinaison linéaire de \(A\) et \(I_2\) puis choisir \(\lambda\) et \(\mu\) pour que \(T(A)P(A)=I_2\).
Aide méthodologique
2. Effectuer la division euclidienne
\(P(X)=P_{\textrm{car},A}(X)Q(X)+R(X)\) puis en déduire
\(P(A)=P_{\textrm{car},A}(A)Q(A)+R(A)\).
3. Calculer le déterminant de \(P(A)\).
Effectuer puis simplifier le produit \((\lambda A+\mu I_2)P(A)\) où \(\lambda\) et \(\mu\) sont des réels quelconques, enfin choisir convenablement \(\lambda\) et \(\mu\).
Aide à la lecture
\(P(A)\) désigne la matrice \(2A^4-12A^3+19A^2-29A+37I_2\), \(I_2\) étant la matrice unité d'ordre 2.
Solution détaillée
1. \(P_{\textrm{car},A}(X)=\left|\begin{array}{cc}1-X&-1\\2&5-X\end{array}\right|=(1-X)(5-X)+2=X^2-6X+7\)
2. On effectue la division euclidienne demandée :
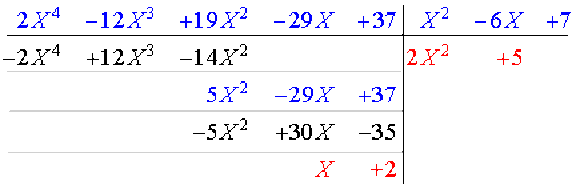
Ainsi \(P(X)=P_{\textrm{car},A}(X)(2X^2+5)+X+2\).
Alors \(P(A)=P_{\textrm{car},A}(A)(2A^2+5I_2)+A+2I_2\), or d'après le théorème de Cayley-Hamilton \(P_{\textrm{car},A}(A)=0\), d'où \(P(A)=A+2I_2\).
Les réels \(\alpha=1\) et \(\beta=2\) conviennent donc.
3. Pour étudier l'inversibilité de la matrice \(P(A)\), on calcule son déterminant :
\(\textrm{det }[P(A)]=\textrm{det }(A+2I_2)=P_{\textrm{car},A}(-2)=(-2)^2-6(-2)+7=23\)
Donc ce déterminant n'est pas nul et la matrice \(P(A)\) est inversible.
On cherche l'inverse de \(P(A)\) sous la forme \(T(A)\), avec \(T(X)=\lambda X+\mu\).
Soit deux réels \(\lambda\) et \(\mu\), si \(T(X)=\lambda X+\mu\) alors
\(T(A)P(A)=(\lambda A+\mu I_2)(A+2I_2)=\lambda A^2+(2\lambda+\mu)A+2\mu I_2\), mais d'après le théorème de Cayley-Hamilton \(A^2-6A+7I_2=0\) donc \(A^2=6A-7I_2\).
Ainsi \(T(A)P(A)=(8\lambda+\mu)A+(-7\lambda+2\mu)I_2\).
Pour trouver l'inverse de \(P(A)\) il suffit de résoudre le système suivant :
\(\left\{\begin{array}{cccccc}8\lambda&+\mu&=0\\-7\lambda&+2\mu&=1\end{array}\right.\). Ce système a une unique solution \(\displaystyle{\lambda=-\frac{1}{23}}\), \(\displaystyle{\mu=\frac{8}{23}}\).
L'inverse de la matrice \(P(A)\) est donc la matrice \(\displaystyle{T(A)=-\frac{1}{23}A+\frac{8}{23}I_2}\).
Autre démonstration
On peut atteindre le résultat plus rapidement en utilisant la division euclidienne du polynôme caractéristique par \(X+2\), reste de la division du polynôme \(P\) par le polynôme caractéristique.
\(P_{\textrm{car},A}(X)=X^2-6X+7=(X-8)(X+2)+23\)
D'où \(P_{\textrm{car},A}(A)=(A-8I_2)(A+2I_2)+23I_2\). En utilisant le théorème de Cayley-Hamilton et le résultat de la question précédente on obtient \((A-8I_2)P(A)+23I_2=0\) et enfin \(\displaystyle{\left[-\frac{1}{23}A+\frac{8}{23}I_2\right]P(A)=I_2}\).