Produit de séries absolument convergentes
Théorème :
On considère deux séries \(\sum u_n\) et \(\sum v_n\) absolument convergentes. Alors la série \(\sum w_n\) où \(w_n=\displaystyle{\sum_{i=0}^n}u_iv_{n-i}\) est absolument convergente et l'on a :
\(\displaystyle{\sum_{n=0}^{+\infty}}w_n=\left(\displaystyle{\sum_{n=0}^{+\infty}}u_n\right)\left(\displaystyle{\sum_{n=0}^{+\infty}}v_n\right)\).
Conseil : Idée de la preuve
Nous donnons seulement une idée de la démonstration qui se fait en deux étapes.
Dans une première étape, on considère le cas où les deux séries \(\sum u_n\) et \(\sum v_n\) sont à termes positifs. On note respectivement \((U_n)\), \((V_n)\) et \((W_n)\) les suites des sommes partielles relatives aux séries \(\sum u_n\), \(\sum v_n\) et \(\sum w_n\), et on établit la double inégalité :
\(W_n\leq U_nV_n\leq W_{2n}\)
illustrée graphiquement ci-dessous.
On représente l'ensemble des couples d'indices \((p, q)\) vérifiant \(p+q\leq n\).
\(W_n=\displaystyle{\sum_{p+q\leq n}}u_pv_q\)
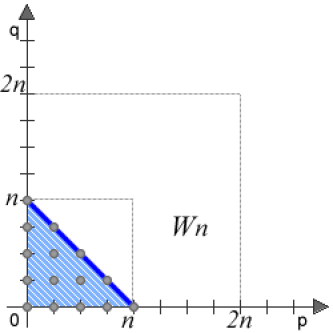
Puis l'ensemble des couples d'indices \((p, q)\) vérifiant \(p\leq n\) et \(q\leq n\)
\(U_n=\displaystyle{\sum_{p\leq n}}u_p\) \(V_n=\displaystyle{\sum_{q\leq n}}v_q\)
\(U_nV_n=\displaystyle{\sum_{p\leq n}}u_p\displaystyle{\sum_{q\leq n}}v_q=\displaystyle{\sum_{p\leq n,q\leq n}}u_pv_q\)
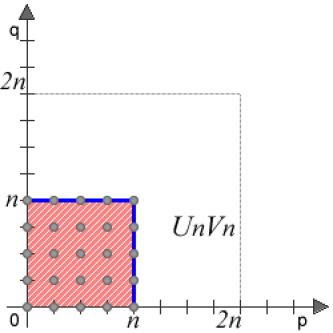
Enfin, l'ensemble des couples d'indices \((p, q)\) vérifiant \(p+q\leq 2n\).
\(W_{2n}=\displaystyle{\sum_{p+q\leq 2n}}u_pv_q\)
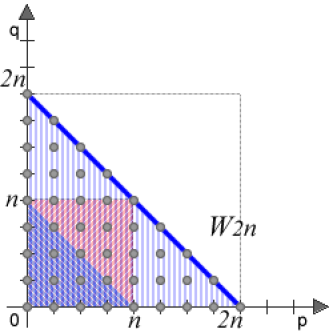
On montre alors à la fois que, la suite \((W_n)\) étant bornée, la série \(\sum w_n\) est convergente, et que la somme de la série \(\sum w_n\) est le produit des sommes des séries \(\sum u_n\) et \(\sum v_n\).
La seconde étape concerne le cas général où les séries \(\sum u_n\) et \(\sum v_n\) sont de signe quelconque et absolument convergentes l'une et l'autre. On applique la première partie aux séries \(\sum|u_n|\), \(\sum|v_n|\) et \(\sum|w_n|\), ce qui permet de conclure à l'absolue convergence de la série \(\sum|w_n|\). Puis on montre, en gardant les notations précédentes que la différence \(|U_nV_n-W_n|\) tend vers 0.
Remarque :
Le théorème reste vrai quand on suppose une seule des séries \(\sum u_n\) ou \(\sum v_n\) absolument convergente, l'autre étant simplement convergente. Il est faux, en revanche, quand les deux séries sont convergentes sans être absolument convergentes (on le verra en exercice en considérant le produit de la série harmonique alternée par elle-même. La série obtenue est divergente).