Loi d'Ohm

Si on maintient une différence de potentiel constante ( \(V_B - V_A\) ) entre les extrémités d'un fil conducteur, on observe donc un champ électrique \(\vec E\) dans ce conducteur, dirigé dans le sens des potentiels décroissants. Chaque charge mobile de valeur q est alors soumise à une force électrique \(\vec F_E=q.\vec E\) de même sens que \(\vec E\) si \(q> 0\) (sens conventionnel du courant).

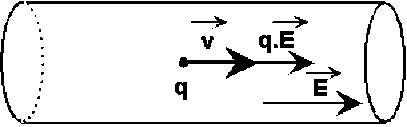
Or un système soumis à une seule force constante a un mouvement uniformément accéléré. Si la force \(\vec F_E\) agissait seule on devrait avoir dans le circuit un courant dont l'intensité augmente indéfiniment dans le temps. Puisque l'on observe au bout d'un certain temps une intensité constante, c'est que la vitesse d'entraînement des charges se stabilise, donc qu'apparaissent dans le conducteur des forces qui équilibrent la force créée par le champ électrique. Par analogie avec les systèmes mécaniques, on peut décrire la résultante de ces forces comme un frottement visqueux : \(\vec F_f=-k.\vec v\)

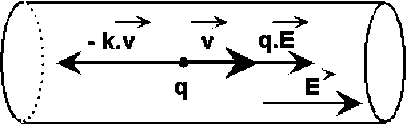
Une étude microscopique montre que \(k=\frac{m}{\tau}\), où m est la masse du porteur de charge et \(\tau\) son temps de relaxation, qui est égal à la durée moyenne séparant deux chocs successifs du porteur de charge dans le matériau.

Ordre de grandeur: \(\tau = 10^{-14}\textrm{s}\)  pour les métaux

\(10^{-13}\) à \(10^{-12}\) s pour les semi conducteurs

En régime permanent, la somme des forces appliquée au porteur de charge est nulle, donc :

\(\vec F_E+\vec F_f=\vec0 \Leftrightarrow q.\vec E-k.\vec v=\vec0 \Leftrightarrow \vec v=\frac{q.\vec E}{k}=q.\frac{\tau}{m}.\vec E\)

\(\textrm{ d'où : }\vec v=\mu.\vec E~\textrm{ avec }~\mu=\frac{q.\tau}{m}\)

\(\mu\) est appelée mobilité de la charge. Un porteur de charge est donc d'autant plus mobile dans un matériau que sa masse est faible, que sa charge est grande, et que la durée qui s'écoule entre deux collisions est importante.