Loi d'Ohm

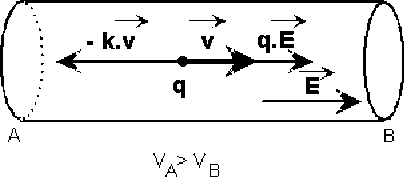
Soit un conducteur^[1] dont les extrémités A et B sont portées à des potentiels différents \(V_A\) et \(V_B\) ( \(V_A > V_B\) ).Nous avons vu qu'à l'intérieur du conducteur un porteur de charge est soumis à une force électrostatique \(\vec F_E=q.\vec E\) et à une force de frottement \(\vec F_f=-k.\vec v\), dont la somme est nulle en régime permanent : \(\vec F_E+\vec F_f=\vec0\)

Par définition, la différence de potentiel ( \(V_A - V_B\) ) entre A et B est égale au travail^[2], de A à B, de la force électrostatique \(\vec F_E=q.\vec E\), par unité de charge \((V_A-V_B)=\frac{W_{A \rightarrow B }~(\vec F_E)}{q}\). Puisque \(V_A > V_B\) , ce travail est positif, donc moteur.

Le travail entre A et B de la force de frottement \(\vec F_f=-k.\vec v\) est un travail résistant, donc négatif. Si la conductivité du matériau est indépendante du champ électrique appliqué, ce travail est proportionnel à l' intensité^[3] du courant dans le circuit :

\(\frac{W_{(A \rightarrow B)}(\vec F_f)}{q}=-R.I\)

On dit alors que le conducteur est ohmique. Le coefficient R est appelé résistance^[4] du conducteur (puisqu'il traduit le fait que le matériau du conducteur résiste au passage du courant en freinant les porteurs de charges). Sa valeur est une constante qui ne dépend que des caractéristiques géométriques du conducteur et électriques du matériau.

Comme en régime permanent : \(\vec F_E+\vec F_f=\vec0\), on a donc : \(( V_A - V_B ) - R.I = 0\)

d'où la loi d'Ohm :

\(( V_A - V_B )= R.I\)

La différence de potentiel entre les bornes d'un conducteur ohmique parcouru par un courant est proportionnelle à l'intensité de ce courant. La caractéristique tension-courant

\(( V_A - V_B ) = \textrm{f}(I)\) est une droite passant par l'origine.