Loi des noeuds
Le courant électrique dans un circuit est dû au déplacement des charges électriques. A un noeud d'un circuit, il ne peut y avoir accumulation de charges: la somme des charges arrivant par les différentes branches est égale à la somme de celles qui repartent. En régime continu[1] permanent, pour chaque branche, \(\displaystyle{I = \textrm{d}q/\textrm{d}t = \textrm{c}^\textrm{ste}}\). D'où :
En un noeud d'un réseau, la somme des intensités[2] des courants qui arrivent est égale à la somme des intensités des courants qui repartent.
\(\sum I_\textrm{entrantes}=\sum I_\textrm{sortantes}\)
On peut également choisir une convention de signe et compter, par exemple, positivement les intensités des courants qui arrivent et négativement celles de ceux qui repartent. L'expression de la loi des noeuds devient alors :
En un noeud d'un réseau, la somme algébrique des intensités des courants est nulle.
\(\sum_\textrm{algébrique}I=0 \textrm{ ou } \sum \bar I=0\)
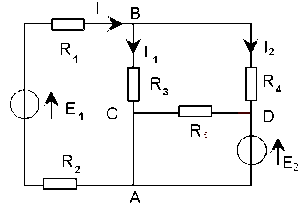
Exemple :
Au noeud B, on peut écrire: \(I = I_1 + I_2 \textrm{ ou }I - I_1 - I_2 = 0\) si on donne des valeurs positives aux intensités; en utilisant la notation algébrique, on aura :
\(\bar I+\bar I_1+\bar I_2=0\textrm{ ou }||\bar I||-||\bar I_1||-||\bar I_2||=0\)
si on choisit comme sens positif celui des courants qui arrivent.