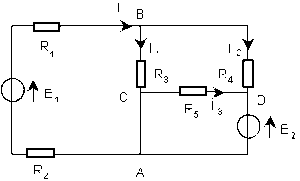
Application de la loi des mailles [Analyse des réseaux linéaires]

Application de la loi des mailles

Les intensités^[1] des courants dans les branches BD, BA, CD, sont des inconnues indépendantes, et les mailles BADB, BCADB, BCDB sont des mailles indépendantes.

maille BCAB:

\(R_3.I_1 + 0 - R_2.I + E_1 - R_1.I = 0\)

maille BCADB:

\(R_3.I_1 + 0 + E_2 + R_4.I_2 = 0\)

maille BCDB:

\(R_3.I_1 -R_5.I_3 + R_4.I_2 = 0\)

qu'on peut écrire:

\(( R_1 + R_2).I + R_3.I_1 = E_1\)

\(R_3.I_1 - R_4.I_2 = E_2\)

\(R_3.I_1 + R_5.I_3 - R_4.I_2 = 0\)

Il y a trois équations et quatre inconnues : pour pouvoir résoudre le problème, il faut une quatrième équation pour éliminer I, qui n'est pas une inconnue indépendante; on utilise donc l'équation au nœud du paragraphe précédent :

\(I - I_1 - I_2 = 0\)

On peut maintenant éliminer I et l'on obtient un système de trois équations à trois inconnues :

\(R_3.I_1 - R_4.I_2 + R_5.I_3 = 0\)

\(R_3.I_1 - R_4.I_2 = E_2\)

\(( R_1 + R_2+ R_3).I_1 + ( R_1 + R_2).I_2 = E_1\)

On résout ensuite ce système, soit par la méthode de substitution^[2], soit par la méthode de Kramer^[3], et l'on obtient :

\(\begin{array}{lll}I_1&=&\frac{R_4.E_1+(R_1+R_2).E_2}{R_3(R_1+R_2)+R_4(R_1+R_2+R_3)}\\\\I_2&=&\frac{R_3.E_1-(R_1+R_2+R_3).E_2}{R_3(R_1+R_2)+R_4(R_1+R_2+R_3)}\\\\I &=& I_1 + I_2 = I_3 = - \frac{E_2}{R_5}\end{array}\);

Notes

Intensité
Grandeur caractérisant un courant électrique, c'est-à-dire un déplacement d'ensemble des charges mobiles dans un conducteur. Unité : l'intensité s'exprime en Ampère (\(\textrm{ A }\))
Relation avec d'autres unités du Système International : l'intensité\( i(t)\) est liée à la charge \(q\) traversant une section du conducteur par la relation : \(i(t)=\textrm{dq}/\textrm{dt}. i(t)\textrm{ en A, q en coulomb (C) , t en seconde (s) }\)
Méthode de substitution
Méthode de résolution d'un système de n équations linéaires à n inconnues, qui consiste à éliminer une inconnue en lui substituant son expression en fonction des autres, puis à répéter l'opération avec une autre inconnue jusqu'à ce qu'il ne reste qu'une équation à une inconnue.
Exemple :
\(3 I_1 + I_2 - I_3 = 6 (1)\)
\(I_1 - I_2 + 3 I_3 = 0 (2)\)
\(-2 I_1 + I_2 + I_3 =0 (3)\)
de (3), on tire : \(I_1 = \frac{1}{2} (I_2 + I_3)\) qui, reporté dans (2),donne :
\(-1/2 I_2 + 7/2 I_3 = 0\) donc \(I_2 = 7 I_3; I_1 = 4 I_3\)
En reportant ces relations dans (1), il vient :
\(12 I_3 + 7 I_3 - I_3 = 6\)
\(18 I_3 = 6\)
\(I_3 = 0.33 A\)
et \(I_2 = 7 I_3 = 2.33 \textrm{A}, I_1 = 4 I_3 = 1.33 \textrm{A}\)
Méthode de Kramer
Méthode de résolution d'un système de n équations linéaires à n inconnues, utilisant les propriétés des matrices
Exemple : le système de 3 équations à 3 inconnues
\(3 I_1 + I_2 - I_3 = 6\)
\(I_1 - I_2 + 3 I_3 = 0\)
\(-2 I_1 + I_2 + I_3 =0\)
a pour écriture matricielle :
\(\displaystyle{\left(\begin{array}{ccc}3&1&-1 \\ 1&-1&3 \\ -2&1&1\end{array}\right)\left(\begin{array}{ccc}I_1 \\ I_2 \\ I_3\end{array}\right)=\left(\begin{array}{ccc}6 \\ 0 \\ 0\end{array}\right)}\)
Chaque inconnue est donnée par le rapport de deux déterminants :
- au numérateur, le déterminant de la matrice (3x3) dans laquelle on a remplacé la colonne correspondant à l'inconnue par la colonne de droite de l'équation.
- au dénominateur, le déterminant de la matrice : \(\displaystyle{\left(\begin{array}{ccc}3&1&-1 \\ 1&-1&3 \\ -2&1&1\end{array}\right)=-18}\)
Ainsi :
\(\displaystyle{I_1 = \frac{\left|\begin{array}{ccc}6&1&-1 \\ 0&-1&3 \\ 0&1&1\end{array}\right|}{-18}=1.33 \textrm{A},\quad I_2=\frac{\left|\begin{array}{ccc}3&6&-1 \\ 1&0&3 \\ -2&0&1\end{array}\right|}{-18}=2.33 \textrm{A},\quad I_3=\frac{\left|\begin{array}{ccc}3&1&6 \\ 1&-1&0 \\ -2&1&0\end{array}\right|}{-18}=0.33 \textrm{A}}\)