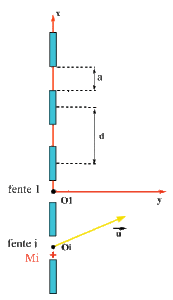
Diffraction par N fentes fines identiques, équidistantes et situées dans un même plan
On cherche à généraliser le cas précédent à \(N\) fentes éclairées sous incidence normale par un même point source pour le même dispositif. Tous les points du plan des fentes sont en phase. Les fentes sont très fines de manière à ce que seule la diffraction due à la largeur soit significative.
Les \(N\) fentes fines ont pour largeur \(a\), pour hauteur \(b\) et sont équidistantes de \(d\).
Soit \(M_i\) un point de la fente \(N_i\) de centre \(O_i\) et repéré par sa côte \(x_{O_i}\).
Soit \(O_1\) le centre de la fente 1 prise pour origine.
\(x_{O_i} = x_{O_1} + \overline{O_1O_i} + x_{O_i}\) ; \(x_{O_1} = 0\)
\(x_{O_i} = \overline{O_1O_i} + x_{O_i}\)
Soit \(\delta_i\) la différence de marche entre la vibration diffractée par \(O_1\) dans la direction \(\vec u\) et celle diffractée par \(M_i\) dans la même direction.
\(\delta_i = \overrightarrow{O_1M_i} ~.~ \vec u = \overrightarrow{O_1O_i} ~.~ \vec u ~+~ \overrightarrow{O_iM_i} ~.~ \vec u\)
En reprenant les notations précédentes :
\(\delta_i = \alpha (N_i - 1) d + \alpha . x_{O_i}\)
\(\Phi_i = \frac{2 \pi \delta_i}{\lambda}\)
La contribution de la fente \(N_i\) à la vibration résultante en \(P\) caractérisé par la direction \(\vec u\) s'écrit :
\(\begin{array}{lll} A_{N_i}(P) & = & \displaystyle{A_0 . b \int_{-\frac{a}{2}}^{\frac{a}{2}} \mathrm e^{j \frac{2 \pi}{\lambda} \big( \alpha (N_i - 1) d + \alpha x_{O_i} \big)} \mathrm d x_{O_i} } \\ & = & A_0 . b . \mathrm e^{j \frac{2 \pi}{\lambda} \alpha (N_i - 1) d } . \frac{\sin \frac{\Phi}{2}}{\frac{\Phi}{2}} \end{array}\)
La contribution des \(N\) fentes est donc :
\(\displaystyle{A(P) = \sum A_{N_i}(P) = A_0 ~ b ~ \frac{\sin \frac{\Phi}{2}}{\frac{\Phi}{2}} \Big( 1 + \mathrm e^{j \frac{2 \pi}{\lambda} d \alpha} + ~ ... ~ + \mathrm e^{j \frac{2 \pi}{\lambda} d \alpha (N - 1) }\Big)}\)
C'est une somme en progression géométrique de raison : \(\mathrm e^{j \frac{2 \pi}{\lambda} d \alpha}\)
\(A(P) = A_0 ~ b ~ a ~ \frac{\sin \frac{\Phi}{2}}{\frac{\Phi}{2}} ~.~ \frac{1 ~-~ \mathrm e^{j \frac{2 \pi}{\lambda} \alpha N d}}{1 ~-~ \mathrm e^{j \frac{2 \pi}{\lambda} \alpha d}}\)
L'intensité en \(P\) est :
\(I(P) = A(P) . A^{\ast}(P) = I_0 ~ a^2 ~ b^2 \left( \begin{array}{c} \frac{\sin \frac{\Phi}{2}}{\frac{\Phi}{2}} \end{array} \right)^2 . \frac{ \sin^2 \Big(N \frac{2 \pi \alpha d}{\lambda}\Big) }{ \sin^2 \Big(\frac{2 \pi \alpha d}{\lambda} \Big)}\)
Sous incidence normale, l'intensité diffractée dans la direction normale au plan du réseau (faisceau obtenu dans le cas de l'optique géométrique) s'écrit, pour \(\alpha = 0\)
\(I_{\alpha = 0}(P) = I_{0N} . N^2\) \(~~ \Rightarrow I_0 ~ b^2 ~ a^2 ~.~ N^2 = I_{0N}\)
et
\(I(P) = \frac{I_{0N}}{N^2} \left( \begin{array}{c} \frac{\sin \frac{\Phi}{2}}{\frac{\Phi}{2}} \end{array} \right)^2 . \frac{ \sin^2 \Big(N \frac{2 \pi \alpha d}{\lambda}\Big) }{ \sin^2 \Big(\frac{2 \pi \alpha d}{\lambda} \Big)}\)