Utilisation des réseaux. Spectres.
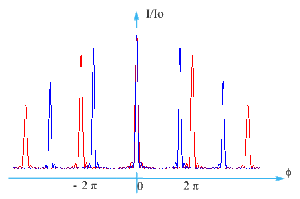
Si la source n'est pas monochromatique on peut observer sur un écran placé dans le plan focal image de la lentille \(L_2\) le spectre de diffraction à l'infini donné par le réseau.
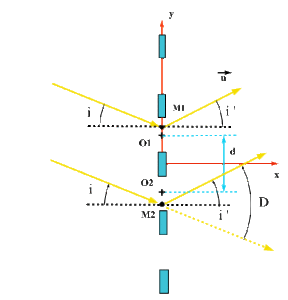
\(\delta = d (\sin i - \sin i')\)
Le maximum d'intensité s'obtient quand : \(\varphi = 2 k \pi = 2 \pi \frac{\delta}{\lambda}\) soit \(\delta = k \lambda\), ce qui correspond à des pics d'intensité fins.
\(k\) est l'ordre d'observation du spectre
\(k = 0\) : la raie centrale est l'image de la source.
On remarque que les raies rouges sont plus déviées que les raies violettes.
En effet \(i\) étant fixé on peut écrire :
\(\sin i' = k \frac{\lambda}{d} - \sin i\)
\(i'\) augmente donc avec \(\lambda\).
Soit \(D\) la déviation d'un rayon diffracté dans la direction \(i'\) et arrivant sous une incidence \(i\). \(D = i' - i\) avec les conventions algébriques habituelles. Fixons \(k\) et \(\lambda\). On a alors un maximum d'intensité pour
\(\delta = k \lambda = d (\sin i - \sin i')\)
Si \(k\) et \(\lambda\) sont fixés alors :
\(\mathrm d \delta = d (\cos i ~.~ \mathrm d i ~-~ \cos i' .~ \mathrm d i') = 0\)
Cherchons l'influence de \(i\) sur la déviation \(D\) :
\(\frac{\mathrm d D}{\mathrm d i} = \frac{\mathrm d i'}{\mathrm d i} - 1 = \frac{\cos i}{\cos i'} - 1 = \frac{\cos i ~-~ \cos i'}{\cos i'}\)
la déviation est extrémale si \(\mathrm d D / \mathrm d i = 0\) donc si :
\(i = i'\) (ordre \(k = 0\) ) ce qui ne présente pas d'intérêt
\(i = - i' \) \(~~\to ~ D_m = 2 i'\)
On vérifie que cet extremum est un minimum de déviation \(D_m\) :
\(D_m = 2 i'\)
\(2 \sin ~ i_m = \frac{k \lambda}{d}\) \(~~ \Rightarrow \sin \frac{D_m}{2} = k \frac{\lambda}{2 d}\)
En conclusion le minimum de déviation dépend du pas du réseau \(d\), de la longueur d'onde \(\lambda\) et de l'ordre d'observation \(k\).
L'intérêt pratique de la mesure de \(D_m\) est important car il permet de mesurer facilement et avec une grande précision \(\lambda\) avec des moyens expérimentaux simples.