Répartition de l'intensité
Le terme \(\left( \begin{array}{c} \frac{\sin \frac{\Phi}{2}}{\frac{\Phi}{2}} \end{array} \right)^2\) est le terme classique étudié dans le cas de la diffraction par une fente fine.
Considérons le terme \(\left( \begin{array}{c} \frac{ \sin \frac{N \varphi}{2} }{ \sin \frac{\varphi}{2} } \end{array} \right)^2\) en posant \(\varphi = \frac{2 \pi \alpha d}{\lambda}\)
\(I(\varphi) = 0\) pour \(\sin \frac{N \varphi}{2} = 0\) et \(\sin \frac{\varphi}{2} \ne 0\)
d'où \(N \frac{\varphi}{2} = p \pi\) avec \(p\) non multiple de \(N\) et \(p \ne 0\)
si \(\sin \frac{\varphi}{2} = 0\) alors
\(\displaystyle{\lim_{\varphi \to 0} I(\varphi) = \left( \begin{array}{c} \frac{ N \frac{\varphi}{2} }{ \frac{\varphi}{2} } \end{array} \right)^2 = N^2}\)
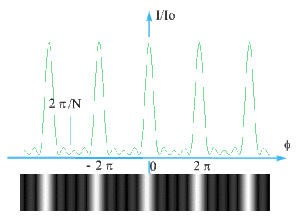
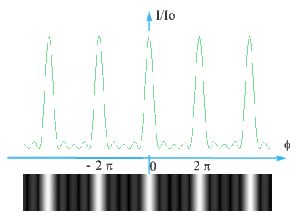
D'où la courbe \(I(\varphi)\) pour \(N = 5\) par exemple.
Entre deux minima nuls les maxima secondaires sont deux fois moins larges que les maxima principaux.
La largeur à la base d'un maximum principal vaut :
\(2 . \frac{2 \pi}{N} = \frac{4 \pi}{N}\)
La largeur à la base d'un maximum secondaire vaut :
\(\frac{2 \pi}{N}\)
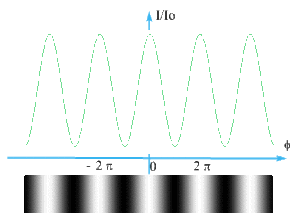
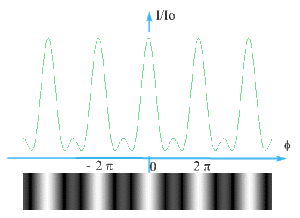
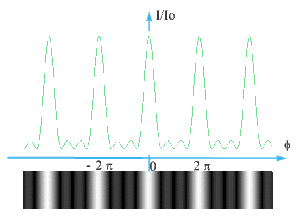
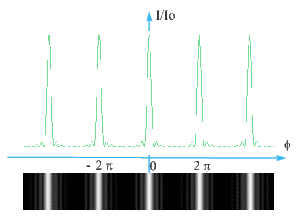
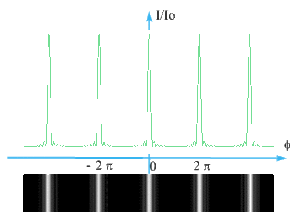
Augmentation progressive du nombre de fentes et observation de la figure d'interférence :
Cas de 2 fentes : \(N=2\)
Cas de 3 fentes : \(N=3\)
Cas de 4 fentes : \(N=4\)
Cas de 5 fentes : \(N=5\)
Cas de 10 fentes : \(N=10\)
Cas de 15 fentes : \(N=15\)
Plus \(N\) est important, plus la largeur des maxima principaux est faible et plus l'intensité des maxima secondaires est petite ( ce résultat est admis afin de ne pas compliquer les calculs).
Pour \(N \to \infty\) on aurait des pics infiniment fins obtenus pour \(\varphi = k 2 \pi\). Les maxima secondaires n'existeraient plus (intensité nulle).
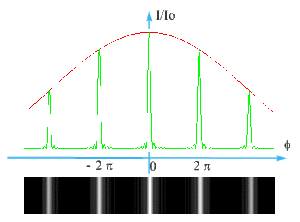
Répartition de l'intensité en tenant compte de la figure de diffraction :
considérons la fonction globale :
\(I = \frac{I_{0N}}{N^2} \left( \begin{array}{c} \frac{\sin \frac{\Phi}{2}}{\frac{\Phi}{2}} \end{array} \right)^2 \frac{ \sin^2 \Big(N \frac{\varphi}{2}\Big) }{ \sin^2 \Big(\frac{\varphi}{2}\Big) }\)
La figure de diffraction module l'intensité des maxima principaux suivant la figure ci-contre.
En conclusion :
- plus les fentes sont fines, plus le profil de diffraction est large et l'intensité des pics principaux diminue ;
- plus le nombre total de fentes éclairées est important et plus les pics sont fins.
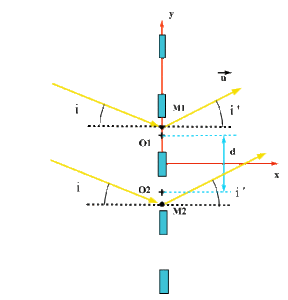
Si le réseau n'est plus éclairé en incidence normale, la différence de marche entre deux rayons issus du centre de deux fentes consécutives s'écrit :
\(\delta = d (\sin i - \sin i')\)
\(i\) et \(i'\) sont comptés algébriquement. Ici \(i'\) est positif et \(i\) est négatif, le sens positif étant choisi habituellement dans le sens trigonométrique direct.
La diffraction obtenue à partir de \(N\) fentes fines est visualisée dans l'animation suivante :
Vous avez la possibilité dans l'animation suivante de faire varier le nombre de fentes entre 2 et 10, leur écartement et la longueur d'onde de la lumière incidente :