Expression générale d'un flux
Durée : 1 mn
Note maximale : 10
Question
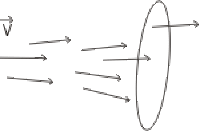
Quelle est l'expression générale du flux d'un champ de vecteurs \(\vec V\) à travers une surface ?
Solution
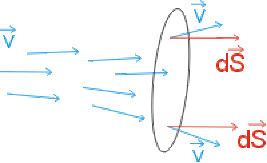
Il faut :
Orienter la surface \(S\) et la décomposer en petits éléments de surface \(d\vec S\) suffisamment petits pour que \(\vec V\) y soit constant
Orienter les vecteurs \(d\vec S\) perpendiculairement à la surface
Faire la somme intégrale de tous les produits scalaires \(\vec V.d\vec S\) sur toute la surface : \(\Phi=\displaystyle{\iint_S\vec V.d\vec S}\)
Évaluation :
Formule : 2 pts
Présence du point entre \(\vec V\) et \(d\vec S\) pour indiquer le produit scalaire : 2 pts
Présence des flèches sur les deux vecteurs : 2 pts
Signe intégrale double : 2 pts
Présence de \(S\), surface d'intégration en bas de l'intégrale : 2 pts