Flux d'un champ de vecteur uniforme
Durée : 1 mn
Note maximale : 9
Question
Un courant d'eau se déplace avec une vitesse uniforme \(\vec V\left(||\vec v||=2m.s^{-1}\right)\) dans un cadre d'aire \(S=4m^2\)
Quelle est la valeur du flux \(\Phi\) de \(\tilde{A}\) travers le cadre dans les cas \(1\), \(2\) et \(3\) (fig)?
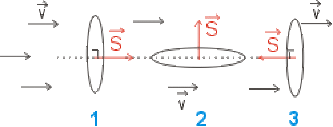
Solution
Le champ de vecteurs étant uniforme, on a simplement : \(\Phi=\overrightarrow{V_m}\vec S\)
cas 1 : \(\Phi=||\vec V||~||\vec S||\cos0=8m^3.s^{-1}\)
cas 2 : \(\Phi=||\vec V||~||\vec S||\cos\frac{\pi}2=0m^3.s^{-1}\)
cas 3 : \(\Phi=||\vec V||~||\vec S||\cos\pi=-8m^3.s^{-1}\)
Evaluation : pour chaque cas : 3pts