Flux d'un champ de vecteurs non uniforme
Durée : 2 mn
Note maximale : 10
Question
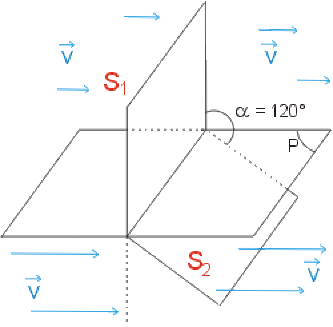
Un courant d'eau traverse deux cadres d'aire \(S_1=S_2=4m^2\) faisant un angle \(\alpha=120°\). Au dessus du plan \(P\) horizontal \(\vec V\) est perpendiculaire au cadre n°1 et \(||V||=2m.s^{-1}\). En dessous de ce plan \(||V||=6m.s^{-1}\).
Quelle est la valeur du flux de \(\vec V\) à travers l'ensemble des deux cadres ?
Solution
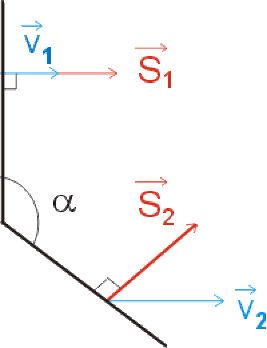
\(\Phi=\overrightarrow{V_1}.\overrightarrow{S_1}+\overrightarrow{V_2}.\overrightarrow{S_2}\)
\(\begin{array}{l} \Phi=\left|\left|\overrightarrow{V_1}\right|\right|.\left|\left|\overrightarrow{S_1}\right|\right|\cos0+\left|\left|\overrightarrow{V_2}\right|\right|.\left|\left|\overrightarrow{S_2}\right|\right|\cos60° \\ \Phi=2\times4\times1+6\times4\times\frac1{2}=20m^3s^{-1} \end{array}\)