Symétrie planaire
Durée : 5 mn
Note maximale : 10
Question
Une plaque de dimension très grande devant la distance d'observation porte une densité superficielle de charge uniforme.
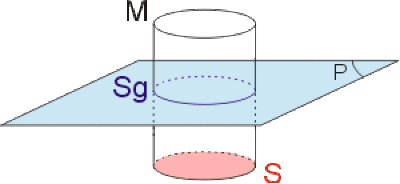
Exprimer le flux de \(\vec E\) à travers \(Sg\) en fonction de \(E\) et \(S\) section droite du cylindre.
Solution
En tout point de la surface, \(\vec E\) est orthogonal à \(d\vec S : \vec E.d\vec S=0\)
Le flux de \(\vec E\) à travers la surface latérale est nul.
En tout point des sections droites \(S_1\) et \(S_2\), \(\vec E\) et \(d\vec S\) sont colinéaires.
\(\Phi=\displaystyle{\iint_{S_1}\vec E.d\vec S +\iint_{S_2}\vec E.d\vec S=\iint_{S_1}E.dS +\iint_{S_2}E.dS}\)
De plus en tout point de \(S_1\) et \(S_2\), \(E\) prend la même valeur par symétrie. D'où \(E\) est une constante vis à vis de la variable d'intégration \(dS\) et peut être sortie de l'intégrale :
\(\Phi= \displaystyle{ \iint_{S_g}\vec E.d\vec S = 2 \iint_{S}E.dS =2E \iint_{S}dS =2ES}\)
10pts