Symétrie planaire
Durée : 3 mn
Note maximale : 10
Question
Une plaque \(P\) de dimension très grande devant la distance d'observation porte une densité superficielle de charges \(\sigma\) uniforme.
Déterminer le champ \(\vec E\) créé en un point \(M\) situé à une distance faible en regard des dimensions de la plaque.
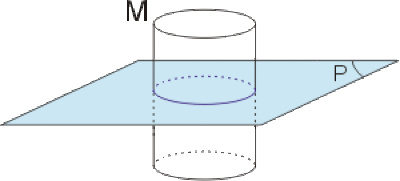
Solution
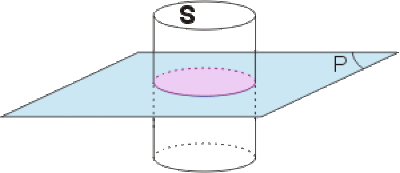
\(\Phi=\displaystyle{\iint_{Sg}\vec E.d\vec S=2ES}\) d'autre part \(\Phi=\frac{Q_{\textrm{int}}}{\epsilon_0}\) (théorème de Gauss) intérieure à \(S_g\) est la charge portée par la zone hachurée sur le plan : \(Q_{\textrm{int}}=\sigma S\)
\(2.E.S=\frac{\sigma S}{\epsilon_0} ; E=\frac\sigma{2\epsilon_0}\).
Le champ est uniforme :
Si \(\sigma>0\), \(\vec E\) s'éloigne du plan.
Si \(\sigma<0\), \(\vec E\) est dirigé vers le plan.