Circulation de E dans un plan 1/4
Partie
Question
Un champ électrostatique est de la forme : \(\vec E = k ~ x ~ \vec u_x\)
a) Exprimer en fonction de \(k\), \(x_1\), \(x_2\) la circulation du champ \(\vec E\) entre deux points \(M_1( x_1, y_0 )\) et \(M_2 ( x_2, y_0 )\).
b) Exprimer en fonction de \(k\), \(x_1\), \(x_2\), \(y_1\) et \(y_2\) la circulation du champ \(\vec E\) entre deux points quelconques \(M_1( x_1, y_1 )\) et \(M_2(x_2, y_2)\).
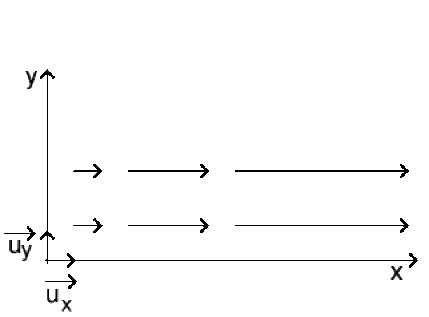
Aide simple
a) \(M_1M_2\) étant parallèle à \(Ox\), un déplacement \(\mathrm d \vec M\) élémentaire sur le parcours \(M_1M_2\) est \(\mathrm d \vec M = \mathrm d x ~ \vec u_x\)
b) Dans le plan, en coordonnées cartésiennes, un déplacement élémentaire \(\mathrm d \vec M\) s'exprime par \(\mathrm d \vec M = \mathrm d x ~ \vec u_x + \mathrm d y ~ \vec u_y\)
Aide détaillée
a)
\(\displaystyle{C = \int_{M_1M_2} \vec E . \mathrm d \vec M = \int_{M_1M_2} k ~ x ~\vec u_x ~ . ~ \mathrm d x ~ \vec u_x = \int_{x_1}^{x_2} k x \mathrm d x}\)
car le produit scalaire \(\vec u_x . \vec u_x = 1\).
\(C = k \Big[ \frac{x^2}{2} \Big]_{x_1}^{x_2} = \frac{k}{2} \big( x_2^2 - x_1^2 \big)\)
b)
\(\displaystyle{C = \int_{M_1M_2} \vec E . \mathrm d \vec M = \int_{M_1M_2} k ~ x ~\vec u_x ( \mathrm d x . \vec u_x + \mathrm d y . \vec u_y ) = \int_{x_1}^{x_2} k x \mathrm d x}\)
car les produits scalaires \(\vec u_x . \vec u_x = 1\) et \(\vec u_x . \vec u_y = 0\) .
\(C = k \Big[ \frac{x^2}{2} \Big]_{x_1}^{x_2} = \frac{k}{2} \big( x_2^2 - x_1^2 \big)\)
Rappel de cours
Voir la page Circulation de E
Solution simple
\(C = \frac{k}{2} \big( x_2^2 - x_1^2 \big)\)
Solution détaillée
a)
\(\displaystyle{C = \int_{M_1M_2} \vec E . \mathrm d \vec M = \int_{M_1M_2} k ~ x ~\vec u_x ~ . ~ \mathrm d x ~ \vec u_x = \int_{x_1}^{x_2} k x \mathrm d x}\)
car le produit scalaire \(\vec u_x . \vec u_x = 1\).
\(C = k \Big[ \frac{x^2}{2} \Big]_{x_1}^{x_2} = \frac{k}{2} \big( x_2^2 - x_1^2 \big)\)
b)
\(\displaystyle{C = \int_{M_1M_2} \vec E . \mathrm d \vec M = \int_{M_1M_2} k ~ x ~\vec u_x ( \mathrm d x . \vec u_x + \mathrm d y . \vec u_y ) = \int_{x_1}^{x_2} k x \mathrm d x}\)
car les produits scalaires \(\vec u_x . \vec u_x = 1\) et \(\vec u_x . \vec u_y = 0\) .
\(C = k \Big[ \frac{x^2}{2} \Big]_{x_1}^{x_2} = \frac{k}{2} \big( x_2^2 - x_1^2 \big)\)