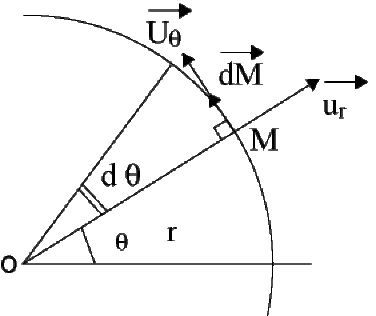
Circulation de E sur un arc de cercle 3/4
Partie
Question
Quelle est la circulation \(C\) du champ électrostatique \(\vec E\) créé par une charge ponctuelle sur un arc de cercle de rayon \(r\) centré sur la charge ?
Aide simple
Le champ \(\vec E\) créé par une charge ponctuelle à la distance \(r\) est \(\vec E = \frac{Q}{4 \pi \epsilon_0 ~ r^2} \vec u_r\)
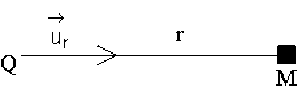
Aide détaillée
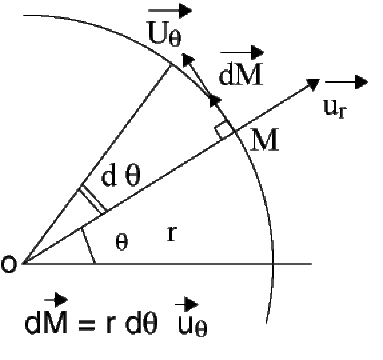
En coordonnées sphériques un déplacement élémentaire sur un cercle de rayon \(r\) s'exprime par :
Rappel de cours
Voir la page Circulation de E
Solution simple
\(\displaystyle{C = \int_{\mathrm{arc}} \vec E . \mathrm d \vec M = 0}\)
car \(\vec E\) est orthogonal à \(\mathrm d \vec M\).
Solution détaillée
\(\displaystyle{C = \int_{\mathrm{arc}} \frac{Q}{4 \pi \epsilon_0 ~ r^2} ~ \vec u_r ~ r ~ \mathrm d \theta ~ \vec u_{\theta}}\)
\(C = 0\) puisque \(\vec u_r\) et \(\vec u_{\theta}\) sont orthogonaux .