Fentes d'Young
Rappel sur : lumière diffractée par une fente fine
La diffraction est un phénomène d'autant plus important que l'ouverture que rencontre le faisceau lumineux monochromatique a des dimensions comparables à la longueur d'onde de ce faisceau.
La diffraction met en évidence la nature ondulatoire de la lumière; les rayons lumineux semblent être déviés au passage de l'ouverture au lieu de se propager en lignes droites dans un milieu transparent, homogène et isotrope.
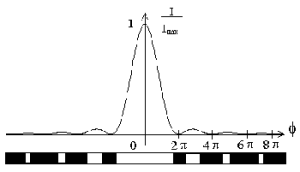
Dans le cas d'une fente étroite de largeur a, éclairée sous incidence normale par une source ponctuelle monochromatique située à l'infini, on observe des franges de diffraction présentant un maximum d'intensité principal centré sur l'image géométrique de la fente et de chaque côté des franges d'intensité plus faible et plus fines.
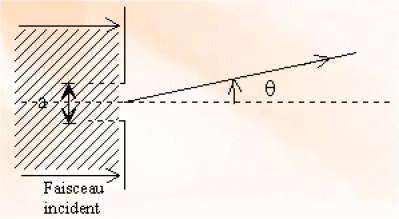
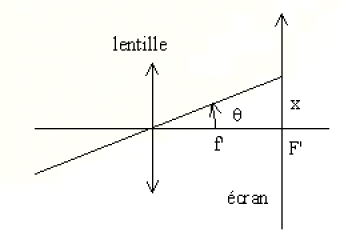
On montre que l'intensité I s'écrit :\(\frac{I}{I_{max}} = \left(\frac{sin \frac{\Phi}{2}} { \frac{\Phi}{2}}\right)^2\) avec \(\Phi=2\frac{\pi}{\lambda}a.sin\theta\), \(\theta\) est la direction d'observation d'un rayon réfracté. Pour un écran plat placé au foyer image d'une lentille convergente de distance focale f' on peut repérer une frange par sa coordonnée x. On a alors \(tan\theta=\frac{x}{f'}\)
Les minima d'intensité sont obtenus pour \(I=0\) soit \(sin\frac{\Phi}{2}=0\) c'est à dire \(sin \theta=m.\lambda\) avec \(m=\pm1,\pm2,\pm3,....\)
Les maxima secondaires sont obtenus pour \(sin\frac{\Phi}{2}=\pm1\)soit pour \(a.sin\theta=\pm\frac{2n+1}{2}.\lambda \)avec \(n=1,2,3,..\)
Le premier maximum secondaire a une intensité relativement faible : \(I_1=0,047.I_{max}\) ; de même le second maximum a une intensité encore plus faible : \(I_2=0,016.I_{max}\).
La plus grande partie de la lumière est située dans le pic principal, deux fois plus large que les pics secondaires.
Etude des fentes d'Young
Deux fentes très fines \(S_1\) et \(S_2\) identiques et parallèles entre elles sont percées dans un écran opaque et éclairées par une fente source \(S\) fine monochromatique et parallèle aux deux fentes \(S_1\) et \(S_2\).
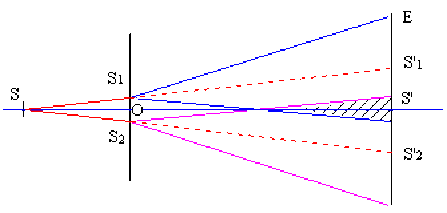
Les deux fentes \(S_1\) et \(S_2\), éclairées par la lumière diffractée par la fente source \(S\), diffractent elles-mêmes la lumière en donnant deux faisceaux centrés sur \(S'_1\) et \(S'_2\).
Elles se comportent donc comme deux sources cohérentes monochromatiques et l'on observe donc un phénomène d'interférences sur un écran \(E\) situé à la distance \(D\) de \(S_1\) \(S_2\) et parallèle aux fentes
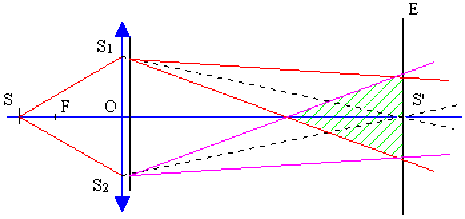
On augmente l'étendue relative du champ d'interférences et la luminosité des franges en modifiant le dispositif précédent : on place pour cela une lentille convergente \(L\) juste avant le plan contenant les fentes \(S_1\) et \(S_2\).
En optique géométrique chaque point \(S\) a une image ponctuelle \(S'\) (dans les conditions de Gauss). De plus le phénomène de diffraction est toujours centré sur l'image géométrique.
Les deux faisceaux diffractés par \(S_1\) et \(S_2\) seront donc centrés sur \(S'\) image de \(S\) et non plus sur \(S'_1\) et \(S'_2\) et présentent donc une partie commune plus importante et plus intense autour de \(S'\).
Complément :
Le dispositif interférentiel des fentes d'Young est visualisé dans l'animation suivante: