Bilentille de Billet
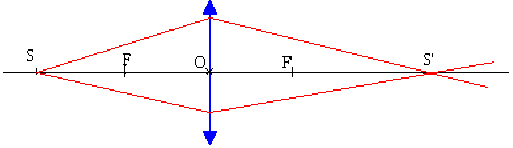
Une lentille mince convergente est sciée en deux suivant un diamètre.
Les deux demi-lentilles sont légèrement écartées l'une de l'autre et légèrement inclinées d'un angle \(\alpha\).
L'espace entre les deux demi lentilles est rendu opaque de manière à éviter une interférence avec les rayons provenant directement de la source mère. On éclaire le dispositif par une source quasi ponctuelle située sur l'axe de la lentille, en avant du foyer objet \(F\).
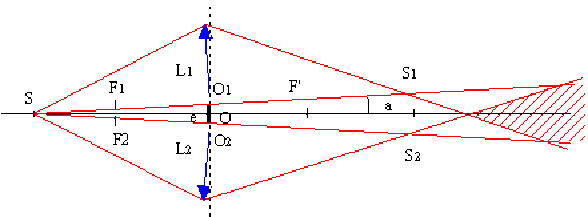
Chaque demi lentille donne de \(S\) une image réelle, quasi ponctuelle. Soient \(S_1\) et \(S_2\) les deux sources secondaires synchrones et cohérentes.
On observera donc les interférences dans la partie commune aux deux faisceaux issus des sources secondaires \(S_1\) et \(S_2\).
Démonstration : Calcul de différence de marche :
Soit \(OO' = d\) la distance de l'écran au centre et e la lentille entre les deux demi-lentilles.
Soit \(\overline{OF'}\) la distacne focale image de la lentille : \(\overline{OF'} = f' = \overline{O_1 F'_1} = \overline{O_2 F'_2}\). Posons \(\overline{O_1S} = p\) et \(\overline{O_1S_1} = p'\)
Les positions de \(S_1\) et \(S_2\) sont données par les formules de conjugaison des lentilles minces :
\(\frac{1}{\overline{O_1S_1}} - \frac{1}{\overline{O_1S }}= \frac{1}{f'} = \frac{1}{p'} - \frac{1}{p}\)
La distance entre les deux sources secondaires \(S_1\) et \(S_2\) s'écrit:
\(\frac{SO}{\epsilon} = \frac{SS_1}{S_1S_2} \Rightarrow S_1S_2 = \frac{SS_1}{SO} . \epsilon = \frac{-p' + p}{p}.\epsilon\) avec \(\overline{SS_1} = \overline{SO_1} + \overline{O_1S_1} = p' - p\)
la différence de marche s'écrit:
\(\delta = \frac{S_1S_2}{d - OS_1}x = \frac{p-p'}{p} . \epsilon .x . \frac{1}{d -p'}\) avec \(\epsilon = 2 \alpha. SO = 2 \alpha |p|\)
Complément :
Le dispositif interférentiel de la bilentille de Billet est visualisé dans l'animation suivante: