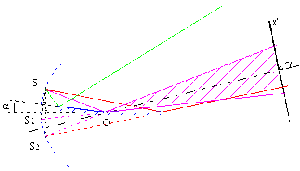
Miroirs de Fresnel

Soit un dièdre formé par deux miroirs plans \(M_1\) et \(M_2\) faisant entre eux un petit angle \(\alpha\).

Soit \(S\) un point source et \(O\) sa projection sur l'arête du dièdre. Le miroir \(M_1\) donne de \(S\) une image symétrique de \(S\) par rapport au miroir plan, ponctuelle et virtuelle. De même le miroir \(M_2\) donne de \(S\) une image \(S_2\). Les points \(S, S_1\) et \(S_2\) se situent alors sur un cercle de centre \(0\) et de rayon \(S_0\) et on a donc: \(S_1OS_2 = 2 \alpha\)

Les deux sources virtuelles \(S_1\) et \(S_2\) sont donc cohérentes et synchrones, la partie commune des deux faisceaux réfléchis par les miroirs \(M_1\) et \(M_2\) permet l'observation d'interférences.On remarque que l'on peut remplacer la source \(S\) par une fente source parallèle à l'arête du dièdre.

Les calculs :

Calcul de la différence de marche \(d :\) on a \(S_1S_2 = 2 \alpha SO = 2 \alpha d \)avec \(SO =d\)

Soit \(D\) la distance de l'écran à l'arête des miroirs \(D = OO'\), alors : \(\delta = \frac{S_1S_2 . x}{D + d}\)

Complément

Le dispositif interférentiel des Miroirs de Fresnel est visualisé dans l'animation suivante:

mfresnel.param [param]

......

Le dispositif interférentiel des Miroirs de Fresnel est également visualisé dans la vidéo suivante:

Miroirs de Fresnel