Biprisme de Fresnel
Définition :
Un biprisme est constitué de deux prismes identiques accolés par la base et de même angle \(A\) très petit (une dizaine de minutes).
Rappel sur le prisme
Il est formé par un milieu réfringent d'indice \(n\), limité par deux faces planes non parallèles se coupant suivant une arête. On appelle plan de section principal tout plan perpendiculaire à l'arête. Les deux faces du prisme forment un angle \(A\).
Définition :
On suppose ici le prisme plongé dans l'air d'indice égal à 1 et on étudie uniquement les rayons lumineux situés dans un plan de section principal.
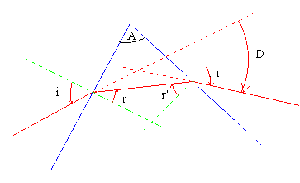
Convention de signe utilisée pour le signe des angles:
concernant le dioptre d'entrée du prisme: l'angle d'incidence \(i\) et de réfraction \(r\) sont comptés positivement dans le sens trigonométrique
pour le dioptre de sortie les angle et \(i'\) sont comptés positivement dans le sens inverse du sens trigonométrique.
On appelle \(D\) l'angle de déviation; c'est l'angle dont il faut tourner le rayon incident pour l'amener dans la direction du rayon émergent. \(D\) est compté algébriquement avec la même convention que pour \(r'\) et \(i'\).
On appelle formules du prisme les quatre formules algébriques suivantes:
Lois de Descartes pour la réfraction
\(\sin i' = n \sin r'\)
\(\sin i = n \sin r\)
Déviation du faisceau
\(A = r + r'\)
\(D = i + i' - (r + r')\)
\(D = i + i' - A\)
Tous les rayons incidents ne peuvent pas émerger du prisme.
En effet la relation \(\sin i = n \sin r\) impose à \(r\) une valeur limite \(l\) telle que: \(1 = n.\sin l\)
Démonstration :
On montre que pour qu'un rayon incident puisse émerger du prisme, il faut vérifier les conditions :
\(A = r + r'\)
\(A < 21\)
\(i \ge io \)avec \(\sin io = n \sin (A-1)\)
Si les angles \(i\) et \(i'\) sont petits alors
\(i = \sin i\) et ( en radians ) \(i = n r'\)
\(i' = \sin i' \)et ( en radians ) \(i' = n r'\)
d'où :
\(D = i + i' - r - r'\)
\(D = nr + nr' - r - r'\)
\(D = (n - 1) (r + r')\)
\(D = (n - 1) A\)
Conclusion
Cette relation est utilisée pour le biprisme de Fresnel.
Etude du biprisme de Fresnel
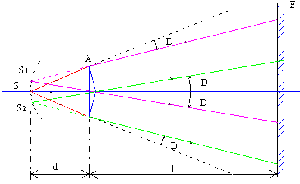
La fente source \(S\) est placée perpendiculairement au plan de section principale du dispositif, sur l'axe du système . Elle éclaire chaque prisme de manière identique qui en donne une image virtuelle supposée stigmatique. On obtient ainsi deux sources virtuelles secondaires \(S_1\) et \(S_2\).
Tous les rayons arrivant sur un prisme sont déviés d'une même quantité \(D = (n - 1)A\) , vers la base du prisme . Tout se passe comme si l'on avait deux fentes sources \(S_1\) et \(S_2\) obtenues par une rotation d'angle \(D\) vers les sommets des prismes.Les interférences s'observent dans la partie commune aux deux faisceaux semblant provenir de \(S_1\) et \(S_2\). Soient \(SP = d\) la distance de la fente source au biprisme et \(PO = 1\) la distance du biprisme à l'écran d'observation.
On a donc : \(S_1S_2 = 2.D.d = 2(n - 1) A.d\)
la différence de marche s'écrit donc : \(\delta = \frac{2 D.\mathrm{d} x}{1 + d} = \frac{2 A (n-1) \mathrm{d} x} {1+d}\)