Tige conductrice sur un plan incliné, soumise à la force de Laplace
Partie
Question
Une tige conductrice (bleue) de longueur \(l\) et de masse \(m\) parcourue par un courant \(I_0\) est déposée sur un plan incliné faisant un angle \(\alpha\) avec l'horizontale. L'ensemble est placé dans un champ magnétique \(\vec B_{\mathrm{ext}}\) constant, uniforme et perpendiculaire à la pente.
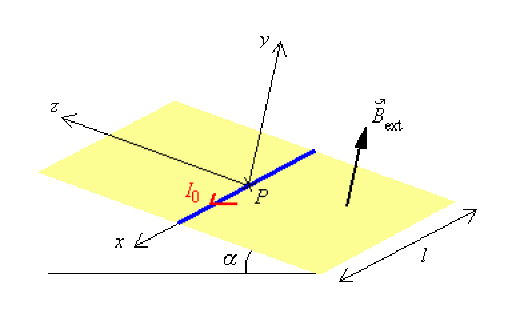
Montrer que la tige peut rester immobile si \(\displaystyle{ m=\frac{I_0.l.B}{\mathrm{g} . \sin\alpha} }\) (\(\mathrm g\) représente l'accélération de la pesanteur).
Les forces de frottements sont négligées.
Aide simple
Calculer d'abord la force de Laplace, faire ensuite le bilan des forces qui s'exercent sur la tige et écrire enfin la relation fondamentale de la dynamique pour traduire l'équilibre.
Rappel de cours
Le produit scalaire :
\(\vec A.\vec B=\left(\begin{array}{c} A_1\\A_2\\A_3\end{array} \right)_{\mathcal{B}} . \left(\begin{array}{c} B_1\\B_2\\B_3\end{array} \right)_{\mathcal{B}} =A_1B_1+A_2B_2+A_3B_3\)
Le produit vectoriel :
\(\vec A\wedge\vec B=\left(\begin{array}{c} A_1\\A_2\\A_3\end{array} \right)_{\mathcal{B}} \wedge\left(\begin{array}{c} B_1\\B_2\\B_3\end{array} \right)_{\mathcal{B}} =\left(\begin{array}{c} A_2B_3-A_3B_2\\A_3B_1-A_1B_3\\A_1B_2-A_2B_1\end{array} \right)_{\mathcal{B}}\)
Les opérateurs vectoriels :
Système de repérage cartésien \(\mathcal{B}_{\mathrm{cart.}}(\vec{e_x}, \vec{e_y}, \vec{e_z})\)
gradient : \(\vec{\mathrm{grad}}U\) | divergence : \(\mathrm{div}\vec A\) | rotationnel : \(\vec{\mathrm{rot}}\vec A\) |
\(\left(\begin{array}{c} \displaystyle{ \frac{\partial U}{\partial x} } \\ \displaystyle{ \frac{\partial U}{\partial y} } \\ \displaystyle{ \frac{\partial U}{\partial z} } \end{array} \right)_{\mathcal{B}_{\mathrm{cart.}}}\) | \(\displaystyle{ \frac{\partial A_x}{\partial x}+\frac{\partial A_y}{\partial y}+\frac{\partial A_z}{\partial z} }\) | \(\left(\begin{array}{c} \displaystyle{ \frac{\partial A_z}{\partial y}-\frac{\partial A_y}{\partial z} } \\ \displaystyle{ \frac{\partial A_x}{\partial z}-\frac{\partial A_z}{\partial x} } \\ \displaystyle{ \frac{\partial A_y}{\partial x}-\frac{\partial A_x}{\partial y} }\end{array} \right)_{\mathcal{B}_{\mathrm{cart.}}}\) |
Système de repérage cylindrique \(\mathcal B_{\mathrm{cyl.}}(\vec{e_r},\vec{e_{\theta}},\vec{e_z})\)
gradient : \(\vec{\mathrm{grad}}U\) | divergence : \(\mathrm{div}\vec A\) | rotationnel : \(\vec{\mathrm{rot}}\vec A\) |
\(\left(\begin{array}{c} \displaystyle{ \frac{\partial U}{\partial r} } \\ \displaystyle{ \frac{1}{r} \frac{\partial U}{\partial \theta} }\\ \displaystyle{ \frac{\partial U}{\partial z} } \end{array} \right)_{\mathcal{B}_{\mathrm{cyl.}}}\) | \(\displaystyle{ \frac{1}{r} \frac{\partial (r . A_r) }{\partial r} + \frac{1}{r} \frac{\partial A_{\theta}}{\partial \theta}+\frac{\partial A_z}{\partial z} }\) | \(\left(\begin{array}{c} \displaystyle{ \frac{1}{r} \frac{\partial A_z}{\partial \theta}-\frac{\partial A_ \theta}{\partial z} } \\ \displaystyle{ \frac{\partial A_r}{\partial z}-\frac{\partial A_z}{\partial r} } \\ \displaystyle{ \frac{1}{r} \left( \frac{\partial (r. A_{\theta})}{\partial r}-\frac{\partial A_r}{\partial \theta} \right)} \end{array} \right)_{\mathcal{B}_{\mathrm{cyl.}}}\) |
Nom de l'outil | Comment s'énonce-t-il ? | Quand l'utiliser ? |
Théorème d'Ampère | \(\displaystyle{ \oint_{\mathcal C}\vec B.\vec{\mathrm{d}l}=\mu_0\sum I }\) | Pour calculer \(\vec B\) si la géométrie du problème permet un calcul simple de la circulation de \(\vec B\). |
Loi de Biot et Savart | \(\displaystyle{ \vec B(M)=\frac{\mu_0}{4\pi}\int_{\mathcal D}\vec{\mathrm{d} \mathcal C}(P)\wedge\frac{\vec{PM}}{PM^3} }\) | Pour calculer \(\vec B\) si la géométrie de la distribution ne permet pas une application simple du théorème d'Ampère. |
Relation champ magnétostatique/ potentiel vecteur | \(\vec{B}(M)=\vec{\mathrm{rot}}\vec A(M)\) | Pour calculer \(\vec B\) si \(\vec A\) est connu. |
Définition de la force de Laplace | \(\vec{F_m}=\displaystyle{ \int_{\mathcal D}\vec{\mathrm{d} \mathcal C}(P)\wedge\vec B_{\mathrm{ext}}(P) }\) | Pour calculer la force qui s'exerce sur une distribution \(\mathcal D\) soumise à un champ magnétostatique extérieur \(\vec B_{\mathrm{ext}}\) |
Théorème de Maxwell | \(W_{2\leftarrow1}=I . \Phi_c\) | Pour calculer directement le torseur des forces qui agissent sur un circuit. |
Définition du potentiel vecteur | \(\displaystyle{ \vec A(M)=\int_{\mathcal D}\frac{\mu_0}{4\pi}\frac{\vec{\mathrm{d}\mathcal C}(P)}{PM} }\) | Pour calculer \(\vec A\) si la distribution a un haut degré de symétrie. |
Solution détaillée
La force de Laplace peut être déterminée à partir de l'expression :
\(\displaystyle{ \vec F=\int_{\mathcal D}I_0\vec{\mathrm{d}l}(P)\wedge\vec B_{\mathrm{ext}}(P) }\).
C'est la force à laquelle est soumis ce circuit.
Exprimons \(I_0\vec{\mathrm{d}l}(P)\) et \(\vec B_{\mathrm{ext}}\) dans la base \(\mathcal B=(\vec{e_x},\vec{e_y},\vec{e_z})\) :
\(I_0\vec{\mathrm{d}l}(P)=\left(\begin{array}{c} I_0\mathrm{d}l\\0\\0 \end{array}\right)\quad\vec B_{\mathrm{ext}}(P)=\left(\begin{array}{c}0\\B\\0\end{array}\right)\)
Calculons le produit vectoriel :
\(I_0\vec{\mathrm{d}l}(P)\wedge\vec B_{\mathrm{ext}}(P)=\left(\begin{array}{c} I_0\mathrm{d}l\\0\\0 \end{array}\right)\wedge\left(\begin{array}{c}0\\B\\0\end{array}\right)=\left(\begin{array}{c} 0\\0\\I_0\mathrm{d}l.B\end{array}\right)=I_0\mathrm{d}l.B.\vec{e_z}\)
Nous devons maintenant intégrer sur le domaine \(\mathcal{D}\) correspondant à la tige de longueur \(l\).
\(\displaystyle{ \vec F=\int_lI_0\mathrm{d}l.B.\vec{e_z}=I_0l.B.\vec{e_z} }\)
Les forces qui s'exercent sur la tige sont les suivantes : force de Laplace, poids et réaction du plan (pas de frottements).
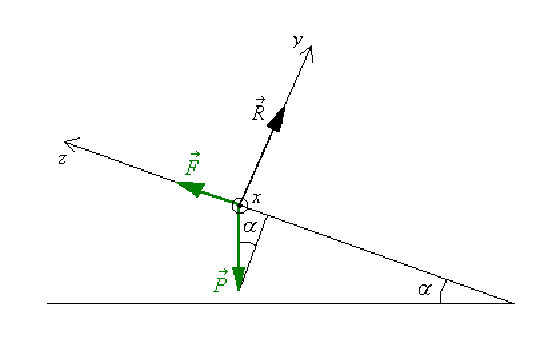
Écrivons la relation fondamentale de la dynamique pour traduire l'équilibre :
\(\vec F+\vec P+\vec R=\vec0\)
Projetons sur l'axe des \(z\) : \(\begin{array}{c} F-P.\sin\alpha=0\\I_0l.B=m \mathrm{g}.\sin\alpha\end{array}\)
D'où \(\displaystyle{ m=\frac{I_0l.B}{\mathrm{g} . \sin\alpha} }\)