Fil rectiligne de longueur finie
Partie
Question
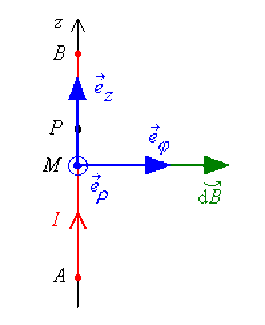
Un fil rectiligne de longueur \(AB\) est parcouru par un courant d'intensité \(I\) circulant de \(A\) vers \(B\).
Nous travaillons dans la base \(\mathcal B=(\vec{e_{\rho}},\vec{e_{\phi}},\vec{e_z})\).
Soient \(M\) le point de coordonnées \((\rho,0,0)\) et \(P\) le point de coordonnées \((0, 0, z)\) associé à l'élément de courant \(I\vec{\mathrm{d}l}\).
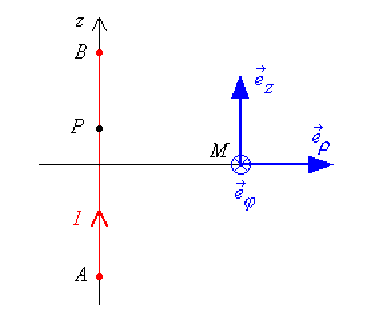
Calculer le champ magnétostatique élémentaire \(\vec{\mathrm{d}B}(M)\) créé par l'élément de courant \(I\vec{\mathrm{d}l}\) au point \(M\) en utilisant la loi de Biot et Savart.
Aide simple
Exprimer les coordonnées dans la base \(\mathcal B=(\vec{e_{\rho}},\vec{e_{\phi}},\vec{e_z})\) des vecteurs \(I\vec{\mathrm{d}l}(P)\) et \(\vec{PM}\) qui interviennent dans la loi de Biot et Savart et calculer leur produit vectoriel.
Rappel de cours
Le produit scalaire :
\(\vec A.\vec B=\left(\begin{array}{c} A_1\\A_2\\A_3\end{array} \right)_{\mathcal{B}} . \left(\begin{array}{c} B_1\\B_2\\B_3\end{array} \right)_{\mathcal{B}} =A_1B_1+A_2B_2+A_3B_3\)
Le produit vectoriel :
\(\vec A\wedge\vec B=\left(\begin{array}{c} A_1\\A_2\\A_3\end{array} \right)_{\mathcal{B}} \wedge\left(\begin{array}{c} B_1\\B_2\\B_3\end{array} \right)_{\mathcal{B}} =\left(\begin{array}{c} A_2B_3-A_3B_2\\A_3B_1-A_1B_3\\A_1B_2-A_2B_1\end{array} \right)_{\mathcal{B}}\)
Les opérateurs vectoriels :
Système de repérage cartésien \(\mathcal{B}_{\mathrm{cart.}}(\vec{e_x}, \vec{e_y}, \vec{e_z})\)
gradient : \(\vec{\mathrm{grad}}U\) | divergence : \(\mathrm{div}\vec A\) | rotationnel : \(\vec{\mathrm{rot}}\vec A\) |
\(\left(\begin{array}{c} \displaystyle{ \frac{\partial U}{\partial x} } \\ \displaystyle{ \frac{\partial U}{\partial y} } \\ \displaystyle{ \frac{\partial U}{\partial z} } \end{array} \right)_{\mathcal{B}_{\mathrm{cart.}}}\) | \(\displaystyle{ \frac{\partial A_x}{\partial x}+\frac{\partial A_y}{\partial y}+\frac{\partial A_z}{\partial z} }\) | \(\left(\begin{array}{c} \displaystyle{ \frac{\partial A_z}{\partial y}-\frac{\partial A_y}{\partial z} } \\ \displaystyle{ \frac{\partial A_x}{\partial z}-\frac{\partial A_z}{\partial x} } \\ \displaystyle{ \frac{\partial A_y}{\partial x}-\frac{\partial A_x}{\partial y} }\end{array} \right)_{\mathcal{B}_{\mathrm{cart.}}}\) |
Système de repérage cylindrique \(\mathcal B_{\mathrm{cyl.}}(\vec{e_r},\vec{e_{\theta}},\vec{e_z})\)
gradient : \(\vec{\mathrm{grad}}U\) | divergence : \(\mathrm{div}\vec A\) | rotationnel : \(\vec{\mathrm{rot}}\vec A\) |
\(\left(\begin{array}{c} \displaystyle{ \frac{\partial U}{\partial r} } \\ \displaystyle{ \frac{1}{r} \frac{\partial U}{\partial \theta} }\\ \displaystyle{ \frac{\partial U}{\partial z} } \end{array} \right)_{\mathcal{B}_{\mathrm{cyl.}}}\) | \(\displaystyle{ \frac{1}{r} \frac{\partial (r . A_r) }{\partial r} + \frac{1}{r} \frac{\partial A_{\theta}}{\partial \theta}+\frac{\partial A_z}{\partial z} }\) | \(\left(\begin{array}{c} \displaystyle{ \frac{1}{r} \frac{\partial A_z}{\partial \theta}-\frac{\partial A_ \theta}{\partial z} } \\ \displaystyle{ \frac{\partial A_r}{\partial z}-\frac{\partial A_z}{\partial r} } \\ \displaystyle{ \frac{1}{r} \left( \frac{\partial (r. A_{\theta})}{\partial r}-\frac{\partial A_r}{\partial \theta} \right)} \end{array} \right)_{\mathcal{B}_{\mathrm{cyl.}}}\) |
Nom de l'outil | Comment s'énonce-t-il ? | Quand l'utiliser ? |
Théorème d'Ampère | \(\displaystyle{ \oint_{\mathcal C}\vec B.\vec{\mathrm{d}l}=\mu_0\sum I }\) | Pour calculer \(\vec B\) si la géométrie du problème permet un calcul simple de la circulation de \(\vec B\). |
Loi de Biot et Savart | \(\displaystyle{ \vec B(M)=\frac{\mu_0}{4\pi}\int_{\mathcal D}\vec{\mathrm{d} \mathcal C}(P)\wedge\frac{\vec{PM}}{PM^3} }\) | Pour calculer \(\vec B\) si la géométrie de la distribution ne permet pas une application simple du théorème d'Ampère. |
Relation champ magnétostatique/ potentiel vecteur | \(\vec{B}(M)=\vec{\mathrm{rot}}\vec A(M)\) | Pour calculer \(\vec B\) si \(\vec A\) est connu. |
Définition de la force de Laplace | \(\vec{F_m}=\displaystyle{ \int_{\mathcal D}\vec{\mathrm{d} \mathcal C}(P)\wedge\vec B_{\mathrm{ext}}(P) }\) | Pour calculer la force qui s'exerce sur une distribution \(\mathcal D\) soumise à un champ magnétostatique extérieur \(\vec B_{\mathrm{ext}}\) |
Théorème de Maxwell | \(W_{2\leftarrow1}=I . \Phi_c\) | Pour calculer directement le torseur des forces qui agissent sur un circuit. |
Définition du potentiel vecteur | \(\displaystyle{ \vec A(M)=\int_{\mathcal D}\frac{\mu_0}{4\pi}\frac{\vec{\mathrm{d}\mathcal C}(P)}{PM} }\) | Pour calculer \(\vec A\) si la distribution a un haut degré de symétrie. |
Solution détaillée
Déterminons \(\vec{\mathrm{d}B}(M)\) en utilisant la loi de Biot et Savart :
\(\displaystyle{ \vec{\mathrm{d}B}(M)=\frac{\mu_0}{4\pi}\left(I\vec{\mathrm{d}l}(P)\wedge\frac{\vec{PM}}{PM^3}\right) }\)
Dans la base \(\mathcal B=(\vec{e_{\rho}},\vec{e_{\phi}},\vec{e_z})\), les coordonnées des différents vecteurs sont :
\(I\vec{\mathrm{d}l}(P)=I\mathrm{d}\vec{OP}=I\mathrm{d}\left(\begin{array}{c}0\\0\\z\end{array}\right)=\left(\begin{array}{c}0\\0\\I . \mathrm{d}z\end{array}\right)\quad \vec{PM}=\left(\begin{array}{c}\rho\\0\\-z\end{array}\right)\) et \(PM^3=\left(\rho^2+z^2 \right)^{3/2}\)
Calculons maintenant \(\displaystyle{ \vec{\mathrm{d}B}(M)=\frac{\mu_0}{4\pi}\left(I\vec{\mathrm{d}l}(P)\wedge\frac{\vec{PM}}{PM^3}\right) }\)
\(\vec{\mathrm{d}B}(M)=\displaystyle{\frac{\mu_0}{4\pi}\frac{1}{\left(\rho^2+z^2\right)^{3/2}}\left(\begin{array}{c}0\\0\\I . \mathrm{d}z\end{array}\right)\wedge\left(\begin{array}{c}\rho\\0\\-z\end{array}\right)=\frac{\mu_0}{4\pi}\frac{1}{\left(\rho^2+z^2\right)^{3/2}}\left(\begin{array}{c}0\\I\rho . \mathrm{d}z\\0\end{array}\right) }\)
Soit : \(\displaystyle{ \vec{\mathrm{d}B}(M)=\frac{\mu_0I}{4\pi}\frac{\rho}{\left(\rho^2+z^2\right)^{3/2}}\mathrm{d}z.\vec{e_{\phi}} }\)