Description du mouvement d'un point matériel
Notion de référentiel
La description du mouvement d'un point matériel exige de connaître sa position dans l'espace à tout instant. Pour cela, en plus du repérage de l'espace physique, il faut définir un phénomène physique (deux passages consécutifs du Soleil au zénith, l'écoulement d'un fluide contenu dans un récipient percé...) appelé chronologie qui permette , à l'aide d'un dispositif de mesure approprié ( réalisant notamment l'entretien du mouvement, le choix de l'unité...) de donner l'information accessible à l'utilisateur : ce dispositif est appelé horloge
La manière de formaliser le repérage du temps est analogue à celle du repérage de l'espace.
L'ensemble repère-horloge constitue un référentiel
La description du mouvement d'un mobile se fait donc dans un référentiel qui doit être défini sans ambiguïté et toujours clairement énoncé.
En résumé, tout observateur est muni d'un temps \(T\) associé à une horloge et d'un espace affine \(E\) (ou vectoriel \(E\)) euclidien orienté à trois dimensions.
Description des mouvements dans l'espace-temps d'un observateur
Supposons qu'il existe des corps suffisamment petits appelés particules pour qu'ils ne coïncident qu'avec un seul point de l'espace.
A tout instant \(t\), il existe un point \(M(t)\) de \(E\) avec lequel coïncide la particule à l'instant \(t\).
Le point \(M(t)\) est la position de la particule \(p\) dans l'espace \(E\) à l'instant \(t\).
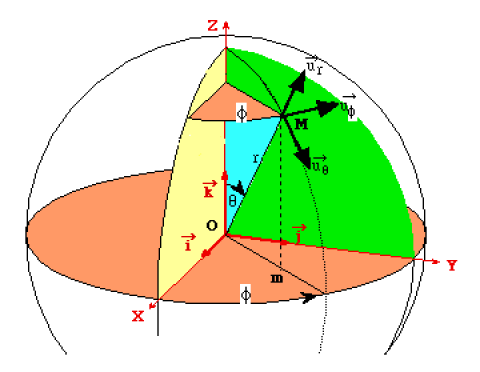
Dans l'espace physique à trois dimensions, il faut trois données pour définir la position d'un point \(M\): ce sont les coordonnées. Par exemple, \(r\), \(\phi\) et \(\theta\) constituent les coordonnées sphériques.
La trajectoire de la particule \(p\) dans \(E\) est l'ensemble de ses positions \(\{M(t)\}\) lorsque \(t\) décrit l'intervalle de définition. Elle est définie par rapport à un référentiel.
Les expressions des coordonnées de \(M\) s'appellent les équations paramétriques du mouvement. En coordonnées cartésiennes, les équations paramétriques de \(M\) sont : \(x(t), y(t), z(t)\) ; en coordonnées cylindriques, elles sont \(\rho(t), \phi(t), z(t)\).
Remarque :
En coordonnées cartésiennes, composantes et coordonnées ont la même expression; dans les autres systèmes de repérage, certaines composantes peuvent être nulles. Par exemple,\(\overrightarrow{OM}=r\overrightarrow{u_r}\) et les composantes de \(\overrightarrow{OM}\) suivant \(\overrightarrow{u_{\phi}}\) et \(\overrightarrow{u_{\theta}}\) sont nulles.
Equation horaire
La trajectoire étant connue, pour repérer le mobile sur cette courbe, on peut choisir une origine \(M_0\) et un sens de parcours (sens positif) : on mesure alors la longueur de l'arc \({\stackrel{\frown}{M_0M}}\) abscisse curviligne \(s\) de \(M\) un nombre algébrique ayant pour valeur absolue la mesure de la longueur de l'arc \({\stackrel{\frown}{M_0M}}\). Si la courbe est fermée (mouvement circulaire par exemple) à une même position de \(M\) peut correspondre une infinité d'abscisses curvilignes.
La fonction \(s(t)\) s'appelle l'équation horaire du mouvement sur la trajectoire.
L'équation de la trajectoire et celle de de l'équation horaire définissent entièrement la position de \(M\) à chaque instant, une fois donnée l'origine \(M_0\); ces équations sont équivalentes à l'équation du mouvement \(\overrightarrow{OM}(t)\). Par contre, l'équation horaire seule (ou celle de la trajectoire) ne suffit pas à définir la position de \(M\) : deux mobiles peuvent se déplacer sur une même trajectoire avec des équations horaires différentes ou avoir des équations horaires identiques sur des trajectoires différentes.
Variations élémentaires du vecteur position
Coordonnées Cartésiennes
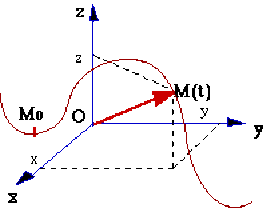
Le vecteur \(\overrightarrow{\delta M}\), variation du vecteur position \(\overrightarrow{OM}\) s'exprime dans la base \((\vec i, \vec j, \vec k)\) : \(\overrightarrow{\delta M}=\delta x\vec i+\delta y\vec j+\delta z\vec k\) où \(\delta x\) (respectivement \(\delta y\), \(\delta z\)) correspondent aux variations de la position lorsque \(x\) (respectivement \(y\), \(z\)) varie seul.
La simulation suivante montre la construction des composantes du point, les vecteurs de base, la variation de chaque coordonnée et la construction de l'élément de volume.
Impossible d'accéder à la ressource audio ou vidéo à l'adresse :
La ressource n'est plus disponible ou vous n'êtes pas autorisé à y accéder. Veuillez vérifier votre accès puis recharger le média.
Coordonnées Cylindriques
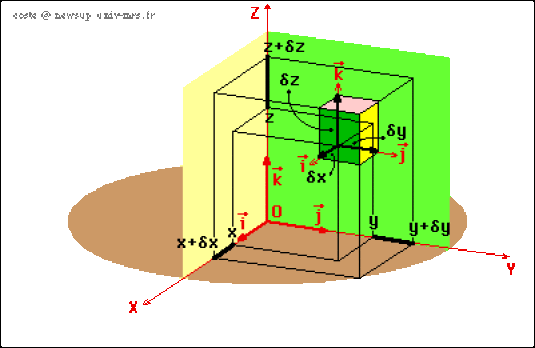
Le vecteur \(\overrightarrow{\delta M}\) : où \(\delta \rho\) (respectivement \(\rho\delta\phi\), \(\delta z\)) correspondent aux variations de la position lorsque \(\rho\) (respectivement \(\phi\), \(z\) ) varie seul.
\(\overrightarrow{\delta M}=\delta\rho\overrightarrow{u_\rho}+\rho\delta\phi\overrightarrow u_\phi+\delta z\vec k\)
La simulation suivante montre la construction des composantes du point, les vecteurs de base, la variation de chaque coordonnée et la construction de l'élément de volume.
Impossible d'accéder à la ressource audio ou vidéo à l'adresse :
La ressource n'est plus disponible ou vous n'êtes pas autorisé à y accéder. Veuillez vérifier votre accès puis recharger le média.
Coordonnées Sphériques
Dans la base sphérique \((\overrightarrow{u_r},\overrightarrow{u_\theta},\overrightarrow{u_\phi})\), le vecteur position s'écrit \(\overrightarrow{OM}=r\overrightarrow{u_r}\)
Le vecteur \(\overrightarrow{\delta M}\), variation du vecteur \(\overrightarrow{OM}\) position s'exprime dans la base \((\overrightarrow{u_r},\overrightarrow{u_\theta},\overrightarrow{u_\phi})\), \(\overrightarrow{\delta M}=\delta r\overrightarrow{u_r}+r\delta\theta\overrightarrow u_\theta+r\sin\theta\delta\phi\overrightarrow{u_\phi}\) où \(\delta r\) (respectivement \(r\delta \theta\), \(r\sin\theta \delta \phi\)) correspondent aux variations de la position lorsque \(r\) (respectivement \(\theta\), \(\phi\)) varie seul.
La simulation suivante montre la construction des composantes du point, les vecteurs de base, la variation de chaque coordonnée et la construction de l'élément de volume.
Impossible d'accéder à la ressource audio ou vidéo à l'adresse :
La ressource n'est plus disponible ou vous n'êtes pas autorisé à y accéder. Veuillez vérifier votre accès puis recharger le média.
Base locale du mouvement
Soit un mobile \(M\) sur une trajectoire \((C)\), courbe, orientée, non "pathologique", qu'il décrit dans le sens positif. Considérons trois positions successives très voisines \(M\),\( M'\) et \(M''\) correspondant à des instants \(t\), \(t'\) et \(t''\) tels que \(t'= t + \Delta t\), \(t'' = t'+ \Delta t\)
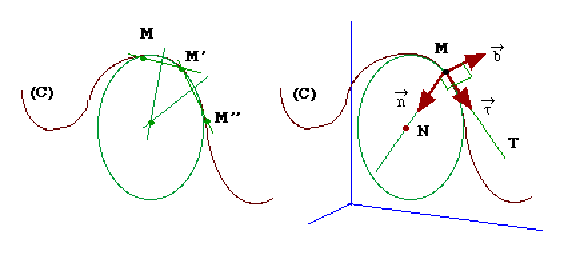
Bien que la courbe \((C)\) ne soit en général pas plane (on parle alors de courbe gauche), les trois points considérés définissent un plan \(P\) et un seul. De même par ces trois points passe un cercle situé dans \(P\) et dont le centre est déterminé par l'intersection des médiatrices des cordes \(MM'\) et \(M'M''\). Ce cercle est circonscrit à \(MM'M''\).
Quand \(\Delta t\) tend vers zéro :
les axes définis par \(\overrightarrow{MM'}\) et \(\overrightarrow{M'M''}\) tendent vers la tangente orientée \(MT\).
le plan \(P\) tend vers un plan dit plan osculateur à \((C)\) en \(M\).
le cercle tend vers le cercle osculateur dont le rayon est le rayon de courbure \(R\) de \((C)\) en \(M\); son centre \(N\) est le centre de courbure.
\(MN\) est orthogonale à \(MT\).
\(MN\) est la normale principale à \((C)\) en \(M\) et \(MT\) est la tangente au cercle en \(M\).
L'inverse \(K=1/R\) du rayon de courbure est la courbure.
Le vecteur unitaire porté par la tangente orientée \(MT\) est \(\vec\tau\).
Le vecteur unitaire porté par la normale principale \(MN\) est \(\vec n\).
Le plan normal est le plan orthogonal à \(\vec\tau\) en \(M\) ; il contient évidemment la normale principale \(MN\). On associe à \(\vec\tau\) et \(\vec n\) le vecteur \(\vec b\) unitaire, perpendiculaire en \(M\) au plan osculateur et tel que le trièdre \((\vec\tau,\vec n,\vec b)\) soit direct ; il est appelé parfois vecteur unitaire porté par la binormale.
Ces trois vecteurs \((\vec\tau,\vec n,\vec b)\) constituent la base de Frenet.
C'est une base orthonormée locale qui suit le mobile étudié, et donc dépend du temps.