Accélération du mobile dans un référentiel R
Définition
Définition :
Soit \(\vec v\) le vecteur vitesse de \(M\) à l'instant \(t\) et \(\vec v'\) en \(M'\) à l'instant \(t'\).
Par définition on appelle vecteur accélération du mobile \(M\) dans le référentiel¸ \([R]\) le vecteur : \(\vec y=\lim_{ {(t'}\rightarrow {t)}}\displaystyle\frac{\vec v'-\vec v}{ t'- t}\)
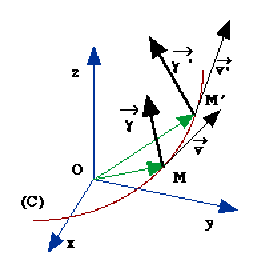
Par définition cette limite est la dérivée du vecteur vitesse par rapport au temps, c'est à dire aussi la dérivée seconde du rayon vecteur ; l'application du mouvement doit donc être deux fois dérivable par rapport au temps : \(\vec y=\displaystyle\frac{ d\vec v} {dt}=\displaystyle\frac{ d^2\vec r}{ {dt}^2}\)
Unité
Du point de vue dimension une accélération est le rapport d'une vitesse à un temps \([\gamma] =VT^{-1}= LT^{-1}T^{-1} = LT^{-2}\)
Dans le système SI, une accélération se mesure en mètre par seconde carré ( \(ms^{-2}\)).
Accélération normale et accélération tangentielle
Nous venons de voir que : \(\vec v=\displaystyle\frac{ {ds}} {dt}\vec\tau= v\vec\tau\)
Dérivons pour obtenir l'accélération : \(\vec\gamma=\displaystyle\frac{ d\vec v} {dt}=\displaystyle\frac{ d^2 s}{ {dt}^2}\vec\tau+\displaystyle\frac{ {ds}} {dt}\displaystyle\frac{ d\vec\tau} {dt}\)
Or : \(\displaystyle\frac{ d\vec\tau} {dt}=\displaystyle\frac{ d\vec\tau} {ds}\displaystyle\frac{ {ds}} {dt}\) donc \(\vec\gamma=\displaystyle\frac{ d^2 s}{ {dt}^2}\vec\tau+\bigg(\displaystyle\frac{ {ds}} {dt}\bigg)^2\displaystyle\frac{ d\tau} {ds}\)
Il nous reste à déterminer \(\displaystyle\frac{ d\vec\tau} {ds}\)
Le vecteur \(\displaystyle\frac{ d\tau} {ds}\) est la limite lorsque \(\Delta s \to 0\) de \(\displaystyle\frac{\vec\tau'-\vec\tau}{\Delta s}=\lim_{(\Delta s\rightarrow0)}\displaystyle\frac{\overrightarrow{\Delta\tau}}{\Delta s}\)
Mais \(\vec\tau\) est obtenu à partir de la limite \(\overrightarrow{ {MM'}}\) de et \(\vec\tau'\) à partir de la limite de \(\overrightarrow{ {M'M''}}\).
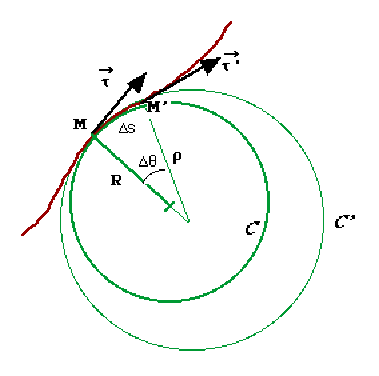
Considérons le cercle \(C'\) de rayon \(r\) passant par \(M, M'\).
A l'arc \(\Delta s\) correspond l'angle \(\Delta \theta\) tel que \(\Delta s= \rho.\Delta \theta\)
On peut écrire : \(\displaystyle\frac{\Delta\vec\tau}{\Delta s}=\displaystyle\frac{\Delta\vec\tau}{\Delta\theta}\displaystyle\frac{\Delta\theta}{\Delta s}=\displaystyle\frac{\Delta\vec\tau}{\Delta\theta}\displaystyle\frac1\rho\)
pour \(\Delta s\to 0\), \(\rho\to R\) le cercle \(C'\) tend vers le cercle osculateur \(C\) de rayon \(R\), d'où : \(\lim_{(\Delta s\rightarrow0)}\displaystyle\frac{\Delta\vec\tau}{\Delta s}=\displaystyle\frac{ d\vec\tau}{ d s}=\displaystyle\frac{ d\vec\tau}{ d\theta}\displaystyle\frac{ d\theta}{ {ds}}=\displaystyle\frac{ d\vec\tau}{ d\theta}\displaystyle\frac1 R\)
\(\frac{d\vec{\tau}}{d\theta}\) est la dérivée d'un vecteur unitaire tangent à un cercle, par rapport à l'angle qui détermine sa position. C'est le vecteur normal \(\vec{n}\). Par suite:
\(\frac{d\vec{\tau}}{d\theta}=\frac{n}{R}\)
On a donc : \(\vec{\gamma}=\frac{d^2s}{dt^2}\vec{\tau}+\frac{v^2}{R}\vec{n}\) avec \(\frac{ds}{dt}=v\) et \(\frac{d^2s}{dt^2}=\frac{dv}{dt}\)
Le vecteur accélération se décompose en :
- une accélération tangentielle \(\frac{d^2s}{dt^2}\vec{\tau}\) de même direction que la vitesse (mais pas forcément de même sens, suivant le signe de la dérivée seconde)
La simulation suivante montre l'accélération tangentielle d'un mouvement circulaire non uniforme :
Impossible d'accéder à la ressource audio ou vidéo à l'adresse :
La ressource n'est plus disponible ou vous n'êtes pas autorisé à y accéder. Veuillez vérifier votre accès puis recharger le média.
- une accélération normale \(\frac{v^2}{R}\vec{n}\) dirigée vers le centre de courbure de la trajectoire.
L'accélération tangentielle est liée à la variation de \(v\) (dérivée de l'abscisse curviligne) et l'accélération normale à la vitesse devariation de la direction du vecteur vitesse .
La simulation suivante montre l'accélération normale d'un mouvement circulaire non uniforme :
Impossible d'accéder à la ressource audio ou vidéo à l'adresse :
La ressource n'est plus disponible ou vous n'êtes pas autorisé à y accéder. Veuillez vérifier votre accès puis recharger le média.
Par exemple, l'indicateur de vitesse d'une voiture donne la valeur instantanée de la vitesse (c'est-à-dire la "vitesse horaire"; dérivée par rapport au temps de l'abscisse curviligne).
L'étude des variations de cette vitesse horaire ne pourra donner que l'accélération tangentielle. L'accélération normale est liée non seulement à la vitesse horaire, mais aussi à la courbure de la trajectoire (qui n'est pas enregistrée par le compteur).
Mouvement uniforme
Par définition un mouvement est dit uniforme si son équation horaire est linéaire : \(s = at +b\), donc si sa vitesse horaire \(a\) est constante.
En conséquence, dans un mouvement curviligne uniforme l'accélération tangentielle \(dv/dt\) est nulle, mais pas en général l'accélération normale, sauf si la trajectoire est rectiligne.