Vitesse du mobile dans un référentiel R
Définition
Définition :
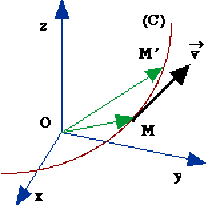
Soit un mobile sur une trajectoire \((C)\) :
à l'instant \(t\), il est en \(M\)
à l'instant \(t'= t + \Delta t\), il est en \(M'\)
Par définition on appelle vecteur vitesse instantanée du mobile par rapport au référentiel \([R]\) :
\(\vec v(t)=\lim(\Delta t\rightarrow 0)\frac{\overrightarrow{MM'}}{\Delta t}\)
\(\vec v(t)=\lim(\Delta t\rightarrow 0)\frac{\overrightarrow{OM'}-\overrightarrow{OM}}{\Delta t}=\lim(\Delta t\rightarrow 0)\frac{\Delta\overrightarrow{OM}}{\Delta t}\)
Par définition, cette limite est la dérivée du rayon vecteur \(\vec r=\overrightarrow{OM}\) par rapport au temps, elle se note : \(\vec v=\frac{d\overrightarrow{OM}}{dt}=\frac{d\vec r}{dt}\)
Il résulte de la définition que \(\vec v\) est un vecteur tangent en \(M\) à la trajectoire.
Compte tenu de la définition de la vitesse et en introduisant l'abscisse curviligne, on peut écrire puisque \(s\) dépend de \(t\).
Mais par définition : \(\frac{d\overrightarrow{OM}}{dt}=\lim_{(\Delta s\rightarrow 0)} \frac{\overrightarrow{MM'}}{\Delta s}\)
Quand \(\Delta s\) tend vers \(0\), la norme \(\frac{\parallel\overrightarrow{MM'}\parallel}{\Delta s}\) de ce vecteur tend vers 1.
(\(\parallel\overrightarrow{MM'}\parallel\) est la longueur de la corde \(MM'\) et \(\mid\Delta s\mid\) est la longueur de l'arc \(\stackrel{\frown}{MM'}\); lorsque \(s'\) tend vers \(s\), \(M'\) tend vers \(M\), la corde tend vers l'arc).
Sa direction est celle de la tangente orientée \(MT\), donc : \(\displaystyle\frac{d\overrightarrow{OM}}{ds}=\vec\tau\)
De la définition de la vitesse, on déduit : \(\vec v=\frac{ds}{dt}\vec\tau=v\vec\tau\) en posant \(v=\displaystyle\frac{ds}{dt}\)
La dérivée par rapport à une variable scalaire \(t\) d'une fonction vectorielle se calcule en exprimant cette fonction vectorielle sur une base.
Dérivée par rapport à ø d'un vecteur :
Soit un vecteur \(\vec v\) faisant l'angle variable \(\phi\) avec une direction fixe.
La dérivée par rapport à \(\phi\) du vecteur unitaire \(\vec v\) est un vecteur unitaire déduite de \(\vec v\) par rotation de \(\displaystyle\frac{+\pi}2\) dans le sens des \(\phi\) croissants.
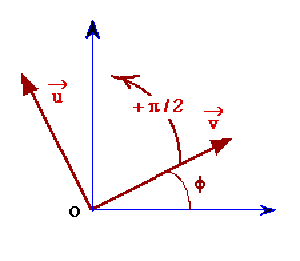
\(\frac{\partial\vec v}{\partial\phi}=\vec u\)
Unité
Du point de vue dimension ,une vitesse est le rapport d'une longueur à un temps: \([v]=LT^{-1}\)
Dans le système SI, une vitesse se mesure en mètre par seconde (\(m/s\) ou \(m.s^{ -1}\)).
Résultat général
Les expressions du vecteur vitesse s'obtiennent aisément à partir des expressions des variations élémentaires du vecteur position dans les divers systèmes de coordonnées \(\vec v=\lim_{\Delta t\rightarrow 0}=\frac{\overrightarrow{OM'}-\overrightarrow{OM}}{\Delta t}=\lim_{\Delta t\rightarrow 0}\frac{\Delta\overrightarrow{OM}}{\Delta t}\)