Mouvements à accélération centrale
On dit que l'accélération est centrale lorsque "le support" du vecteur accélération passe constamment par un point fixe appelé centre des accélérations.
Ces mouvements à accélération centrale ont une grande importance en mécanique, on peut citer comme exemple le mouvement des planètes et des satellites artificiels, des électrons dans les atomes etc....
Vitesse aréolaire
Considérons un mobile M décrivant dans un référentiel \(R( O, \vec i, \vec j, \vec k)\) un mouvement à accélération centrale.
Il est commode de choisir l'origine du repère confondu avec le centre des accélérations \(O\).
Le rayon vecteur \(\overrightarrow{ {OM}}\) et l'accélération \(\vec\gamma\) étant constamment colinéaires, on peut écrire : \(\overrightarrow{ {OM}}\wedge\vec\gamma=\vec0\) (1)
Considérons alors le produit vectoriel \(\overrightarrow{ {OM}}\wedge\vec v\) que nous dérivons par rapport au temps pour faire apparaitre : \(\overrightarrow{ {OM}}\wedge\vec\gamma\)
On obtient : \(\frac{ d(\overrightarrow{ {OM}}\wedge\vec v)} {dt}=\frac{ d\overrightarrow{ {OM}}} {dt}\wedge\vec v+\overrightarrow{ {OM}}\wedge\frac{ d\vec v} {dt}\)
Or : \(\frac{ d\overrightarrow{ {OM}}} {dt}=\vec v\) \(\frac{ d\vec v} {dt}=\vec\gamma\)
Par suite : \((\vec v \wedge \vec v) + (\overrightarrow{ {OM}}\wedge\vec\gamma)=\vec0\) d'après (1) soit finalement : \(\frac{ d(\overrightarrow{ {OM}}\wedge\vec v)} {dt}=\vec0\) donc : \(\overrightarrow{ {OM}}\wedge\vec v=\vec C=\)vecteur constant
Par définition le vecteur \(\vec C\) s'appelle le moment du vecteur vitesse du mobile.
La trajectoire est plane
Le vecteur \(\vec C\) étant constant définit une direction invariante ; d'après la définition du produit vectoriel, les vecteurs \(\overrightarrow{ {OM}}\) et \(\vec v\) sont constamment dans le plan perpendiculaire en \(O\) à \(\vec C\) ; par suite, ce plan contient la trajectoire et le centre des accélérations \(O\).
La loi des aires
En coordonnées polaires (cylindriques planes), le rayon vecteur et la vitesse s'écrivent dans le plan \((O_{xy})\) de la trajectoire : \(\overrightarrow{ {OM}}=\rho\vec{ u_\rho}\) et \(\vec v=\rho'\vec{ u_\rho}+\rho\phi'\vec{ u_\phi}\)
Par suite : \(\vec C = \overrightarrow{ {OM}}\wedge\vec v=\rho^2\phi'\vec k\)
Le vecteur \(\vec C\) étant constant, sa norme est constante.
\(C=\rho^2\phi'=cte\)
Examinons dans le plan de la trajectoire l'aire balayée par le rayon vecteur ; entre les instants \(t\) et \(t+\Delta t\) le rayon vecteur passe de \(\overrightarrow{ {OM}}\) à en effectuant une rotation d'angle \(\Delta \phi\).
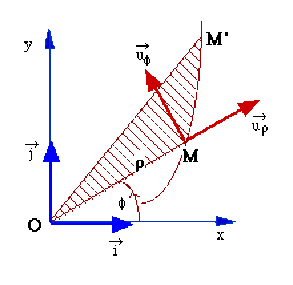
L'aire, hachurée sur la figure, est approchée par celle du triangle \(OMM'\) dont la mesure est : \(\Delta S=\frac{1}2[\overrightarrow{ {OM}}\wedge\overrightarrow{ {OM'}}]\) ou également : \(\Delta S=\frac{1}2[\overrightarrow{ {OM}}\wedge\overrightarrow{ {MM'}}]\) avec \(\overrightarrow{ {OM}}=\rho\vec{ u_\rho}\) et \(\overrightarrow{ {MM'}}=\Delta\rho\vec{ u_\rho}+\rho\Delta\phi\vec{ u_\phi}\)
\(\overrightarrow{ {OM}}\wedge\overrightarrow{ {MM'}}=\rho^2\Delta\phi(\vec{ u_\rho}\wedge\vec{ u_\phi})=\rho^2\Delta\phi\vec k\)
On obtient \(\Delta S=\frac{1}2\rho^2\Delta\theta\)
Nous compterons la surface positivement pour \(\Delta \phi > 0\) (sens trigo) :
Alors quand \(t'\to t\) , \(\Delta S \to {dS}=\frac{1}2\rho^2 d\phi\)
Expression que l'on peut écrire : \({dS}=\frac{1}2\rho^2\frac{ d\phi}{ {dt}} {dt}=\frac{1}2\rho^2\phi' {dt}=\frac{1}2 {Cdt}\)
Il en résulte la relation dite loi des aires et la vitesse de balayage de la surface ou vitesse aréolaire est alors égale à \(C/2\) \(S_\textrm{balay\'ee}=\frac{1}2 ( t- t_0)\)
Le rayon vecteur balaye des aires égales pendant des intervalles de temps égaux.
On appelle \(C\) la constante des aires.
Remarque :
Cette relation est un théorème puisqu'elle est démontrée à partir de l'hypothèse du mouvement à accélération centrale ; on lui garde cependant le nom de loi, car, historiquement, elle a été découverte à partir des relevés de mesures de Kepler sans que l'on ait encore soupçonné la notion d'accélération centrale.
La simulation suivante montre divers mouvements à accélération centrale.
Impossible d'accéder à la ressource audio ou vidéo à l'adresse :
La ressource n'est plus disponible ou vous n'êtes pas autorisé à y accéder. Veuillez vérifier votre accès puis recharger le média.
Formules de Binet
Première formule de Binet sur la vitesse
En coordonnées polaires, la vitesse s'écrit : \(\vec v=\rho'\vec{ u_\rho}+\rho\phi'\vec{ u_\phi}\)
Élevons au carré : \(v^2=\vec v.\vec v=\rho'^2+\rho^2\phi'^2\)
Or : \(\rho'=\frac{ d\rho}{ {dt}}=\frac{ d\rho}{ d\phi}\frac{ d\phi}{ {dt}}\)
Mais la loi des aires montre que : \(\phi'=\frac{ d\phi}{ {dt}}=\frac C{\rho^2}\) ; par suite : \(v^2=\frac{ C^2}{\rho^4}(\frac{ d\rho}{ d\phi})^2+\rho^2\frac{ C^2}{\rho^4}\)
Or on peut écrire : \(\frac1{\rho^4}(\frac{ d\rho}{ d\phi})^2=\Big[\frac d{ d\phi}(\frac1\rho)\Big]^2\)
D'où la première formule de Binet : \(v^2 = C^2\{(\frac1\rho)^2+\Big[\frac d{ d\phi}(\frac1\rho)\Big]^2\}\)
Pour simplifier l'écriture ; on pose en général \(u=\frac1\rho\)
\(v^2= C^2\Big[ u^2+(\frac{ {du}}{ d\phi})^2\Big]\)
Deuxième formule de Binet sur l'accélération
En coordonnées polaires, l'accélération s'écrit, compte tenu du fait que la composante sur \(\vec{ u_\phi}\) est nulle : \(\vec\gamma=(\rho''-\rho\phi'^2)\vec{ u_\rho}\)
On peut éliminer le temps en utilisant la loi des aires : \(\rho''=\frac{ d^2\rho}{ {dt}^2}=\frac d{ {dt}}(\frac{ d\rho}{ d\phi}\frac{ d\phi}{ {dt}})=\frac d{ d\phi}(\frac C{\rho^2}\frac{ d\rho}{ d\phi})\frac{ d\phi}{ {dt}}=\frac{ C^2}{\rho^2}\frac d{ d\phi}(\frac1{\rho^2}\frac{ d\rho}{ d\phi})\)
Mais : \(\frac1{\rho^2}\frac{ d\rho}{ d\phi}=-\frac d{ d\phi}(\frac1\rho)\) ; par suite : \(\rho''=-\frac{ C^2}{\rho^2}\frac{ d^2}{ d\phi^2}(\frac1\rho)\)
Quant à l'expression \(\rho{\phi'}^2\), elle s'écrit , compte tenu de la loi des aires : \(\rho\phi'^2=\rho\frac{ C^2}{\rho^4}=\frac{ C^2}{\rho''}\)
L'accélération prend ainsi la forme : \(\vec\gamma=-\frac{ C^2}{\rho^2}\Big[\frac1\rho+\frac{d^2}{ d\phi^2}(\frac1\rho)\Big]\vec{ u_\rho}\)
En posant de nouveau \(u=\frac1\rho\), on obtient la seconde formule de Binet : \(\vec\gamma=- C^2 u^2\Big[ u+\frac{ d^2 u}{ d\phi^2}\Big]\vec{ u_\rho}\)
Ces relations sont utilisées lors de l'étude de la Dynamique dans un champ central.
Par suite, il est décrit à vitesse aréolaire constante \(= \rho^2\phi' = C\)