Cinétique

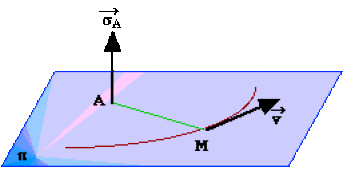
On appelle moment cinétique d'une particule $M$ (ou point matériel) de masse $m$, par rapport à un point $A$ dans le référentiel $R$ le vecteur $\overrightarrow\sigma$ tel que:

$\displaystyle{\overrightarrow\sigma_A=\overrightarrow{AM}\wedge m\overrightarrow v=\overrightarrow{AM}\wedge\overrightarrow p}$

Le moment cinétique est également appelé moment angulaire.

L'équation aux dimensions de la norme du moment cinétique est: $[ \sigma ] = M L^2T^{-1}$

L'unité de moment cinétique est le kilogramme mètre carré par seconde ($\textrm{kg}. \textrm m^2. \textrm s^{ -1}$.)

Calculons le moment cinétique du point matériel $M$ dans le même référentiel $R$ par rapport à un autre point $A'$. La définition s'écrit :

$\displaystyle{\overrightarrow\sigma_{A'}=\overrightarrow{A'M}\wedge m\overrightarrow v}$

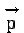
Mais : $\displaystyle{\overrightarrow{A'M}=\overrightarrow{A'A}+\overrightarrow{AM}}$

$\displaystyle{\overrightarrow\sigma_{A'}=\overrightarrow\sigma_A+\overrightarrow{A'A}\wedge\overrightarrow p}$

Le moment cinétique par rapport à un point $A'$ est différent de celui par rapport à un point $A$, même s'il s'agit de la même particule avec la même quantité de mouvement.

On doit toujours préciser par rapport à quel point d'un référentiel on détermine le moment cinétique d'une particule.