Théorèmes généraux

Pour établir ce théorème, nous faisons les deux hypothèses suivantes:

• Le référentiel \([R]\) est galiléen.

• Le point \(A\) est fixe dans le référentiel [\(R\)] ( c'est souvent l'origine du référentiel [\(R\)]).

Dérivons l'expression du moment cinétique du point matériel de masse \(m\), par rapport à un point \(A\) dans le référentiel [\(R\)]; le vecteur \(\overrightarrow\sigma\) est tel que:

\(\displaystyle{\overrightarrow\sigma_A=\overrightarrow{AM}\wedge m\overrightarrow v=\overrightarrow{AM}\wedge\overrightarrow p}\)

\(\displaystyle{\frac{\textrm{d}\overrightarrow{\sigma_A}}{\textrm{dt}}=\frac{\textrm{d}(\overrightarrow{AM}\wedge\overrightarrow p)}{\textrm{dt}}=\frac{\textrm{d}\overrightarrow{AM}}{\textrm{dt}}\wedge\overrightarrow p+\overrightarrow{AM}\wedge\frac{\textrm d{\overrightarrow p}}{\textrm{dt}}\quad(1)}\)

 Appelons \(O\) l'origine du référentiel [\(R\)], par définition :

\(\displaystyle{\overrightarrow v=\frac{\textrm{d}\overrightarrow{OM}}{\textrm{dt}}=\frac{\textrm{d}\overrightarrow{OA}}{\textrm{dt}}+\frac{\textrm{d}\overrightarrow{AM}}{\textrm{dt}}=\frac{\textrm{d}\overrightarrow{AM}}{\textrm{dt}}}\)

car \(A\) est fixe dans [\(R\)]. En appelant \(\overrightarrow F\) la résultante des forces appliquées à \(M\), on a :

\(\displaystyle{\frac{\textrm d\overrightarrow p}{\textrm{dt}}=\overrightarrow F}\)

donc d'après (1) :

\(\displaystyle{\frac{\textrm d\overrightarrow{\sigma_A}}{\textrm{dt}}=\overrightarrow v\wedge m\overrightarrow v+\overrightarrow{AM}\wedge\overrightarrow F}\)

or \(\displaystyle{\overrightarrow v\wedge m\overrightarrow v=\overrightarrow0\textrm{ et }\overrightarrow{AM}\wedge\overrightarrow F=\overrightarrow N(A)}\)

\(\displaystyle{\frac{\textrm{d}\overrightarrow{\sigma_A}}{\textrm{dt}}=\overrightarrow N(A)}\)

Théorème du moment cinétique

Dans un référentiel galiléen, la dérivée par rapport au temps du moment cinétique d'un point matériel par rapport à un point \(A\) fixe dans ce référentiel, est égale au moment résultant par rapport au même point \(A\) des forces appliquées au point matériel.

Nous supposons toujours que le point \(A\) est fixe dans [\(R\)] galiléen. Dérivons par rapport au temps l'expression du moment cinétique :

\(\displaystyle{\frac{\textrm d}{\textrm{dt}}\overrightarrow{\sigma_A}=\sum_{i=1}^N\frac{\textrm d{\overrightarrow{AM_i}}}{\textrm{dt}}\wedge m_i\overrightarrow v_i+\sum_{i=1}^N\overrightarrow{AM_i}\wedge m_i\frac{\textrm{d}}{\textrm{dt}}\overrightarrow{v_i}}\)

Appelons \(O\) l'origine du référentiel [\(R\)], par définition :

\(\displaystyle{\overrightarrow{v_i}=\frac{\textrm{d}\overrightarrow{OM_i}}{\textrm{dt}}=\frac{\textrm{d}\overrightarrow{OA}}{\textrm{dt}}+\frac{\textrm{d}\overrightarrow{AM_i}}{\textrm{dt}}=\frac{\textrm{d}\overrightarrow{AM_i}}{\textrm{dt}}}\)

car \(A\) est fixe dans [\(R\)]. Et par suite :

\(\displaystyle{\frac{\textrm{d}\overrightarrow{\sigma_A}}{\textrm{dt}}=\sum_{i=1}^N\overrightarrow{v_i}\wedge m_i\overrightarrow{v_i}+\sum_{i=1}^N\overrightarrow{AM_i}\wedge m_i\overrightarrow{\gamma_i}=\sum_{i=1}^N\overrightarrow{AM_i}\wedge m_i\overrightarrow{\gamma_i}}\)

Or\( \displaystyle{m_i\overrightarrow{\gamma_i}=\overrightarrow{F}_{iappl}}\) où \(\displaystyle{\overrightarrow F_{iappl}}\) est la résultante des forces appliquées au point \(M_i\); ces forces appliquées se décomposent en forces intérieures au système et forces extérieures :

\(\displaystyle{\overrightarrow F_{iappl}=\overrightarrow F_{iint}+\overrightarrow F_{iext}}\)

et donc : \(\displaystyle{\frac{\textrm{d}}{\textrm{dt}}\overrightarrow{\sigma_A}=\sum_{i=1}^N\overrightarrow{AM_i}\wedge\overrightarrow{F}_{iint}+\sum_{i=1}^N\overrightarrow{AM_i}\wedge\overrightarrow F_{iext}}\)

Or, la somme de tous les moments intérieurs est nulle (ce qui se démontre aisément dans le cas de forces intérieures centrales, opposées deux à deux et telles que\( \displaystyle{\overrightarrow{M_iM_j}}\) soit colinéaire à \(\displaystyle{\overrightarrow F_{ij}}\).

Le même résultat est obtenu pour des forces intérieures quelconques.

\(\displaystyle{\overrightarrow{N}(A)_{int}=\overrightarrow0}\)

d'où

\(\displaystyle{\frac{\textrm{d}\overrightarrow{\sigma_A}}{\textrm{dt}}=\overrightarrow N(A)_{ext}}\)

Théorème du moment cinétique pour un système

Dans un référentiel galiléen, la dérivée par rapport au temps du moment cinétique d'un système matériel pris par rapport à un point fixe \(A\) du référentiel est égale au moment résultant par rapport à \(A\) des seules forces extérieures appliquées au système.

Dans un référentiel galiléen, considérons deux points \(A\) et \(A'\) et calculons les moments cinétiques du système (\(S\)) par rapport à ces deux points dans le même référentiel :

\(\displaystyle{\overrightarrow{\sigma_A}=\sum_{i=1}^N\overrightarrow{AM_i}\wedge m_i\overrightarrow v_i\textrm{ et }\overrightarrow{\sigma_{A'}}=\sum_{i=1}^N\overrightarrow{A'M_i}\wedge m_i\overrightarrow v_i}\)

Ces deux moments cinétiques sont calculés dans \(R\), seul le point de référence change.

Mais\( \displaystyle{\overrightarrow{A'M_i}=\overrightarrow{A'A}+\overrightarrow{AM_i}}\)

Par suite: \(\displaystyle{\overrightarrow{\sigma_{A'}}=\overrightarrow{\sigma_A}+\overrightarrow{A'A}\wedge\sum_{i=1}^Nm_i\overrightarrow v_i\textrm{ avec }\overrightarrow p=\sum_{i=1}^Nm_i\overrightarrow v_i}\)

d'où l'on tire :

\(\displaystyle{\overrightarrow{\sigma_A}=\overrightarrow{\sigma_{A'}}+AA'\wedge\overrightarrow p}\)

Prenons maintenant \(A'\) au centre de masse \(G\) du système auquel on associe son référentiel du centre de masse [\(R_G\)].

\(\displaystyle{\overrightarrow{\sigma_A}=\overrightarrow\sigma_G+\overrightarrow{AG}\wedge\overrightarrow p}\)

Ces deux moments cinétiques sont calculés dans [\(R\)]. Mais nous avons vu que\( \displaystyle{\overrightarrow{\sigma_G}}\) est égal à \(\displaystyle{\overrightarrow{\sigma'_G}}\) , par suite:

\(\displaystyle{\overrightarrow{\sigma_A}=\overrightarrow{\sigma'_G}+\overrightarrow{AG}\wedge\overrightarrow p}\)

Premier Théorème de KOENIG

Le moment cinétique d'un système de points matériels calculé par rapport à un point \(A\) dans un référentiel \([R]\) galiléen est égal au moment cinétique par rapport au centre de masse du système calculé dans le référentiel du centre d'inertie augmenté du moment cinétique par rapport à \(A\) dans le référentiel \([R]\) d'un point matériel confondu avec le centre de masse et où serait concentrée toute la masse du système.

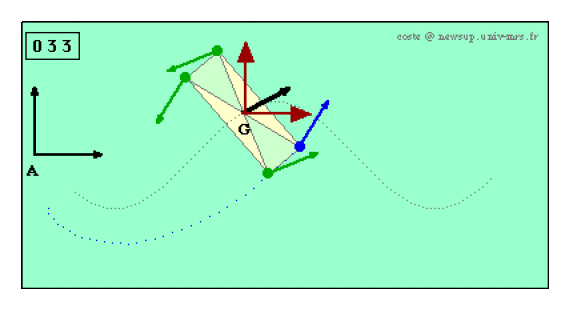
La simulation suivante montre un système matériel non isolé, constitué de quatre masses, dont le centre de masse effectue une trajectoire sinusoïdale; l'ensemble des masses effectue une rotation dans le référentiel barycentrique.