Miroir commercial
Durée : 10 mn
Note maximale : 8
Question
Les miroirs commerciaux sont en général des vitres d'épaisseur \(e\), aluminées face arrière.
comparer l'image donnée par un miroir plan (tel qu'il est défini en optique géométrique) et l'image donnée par un miroir commercial. En déduire le miroir plan équivalent à un miroir commercial d'épaisseur \(e\) et d'indice du verre \(n\).
un observateur placé devant un miroir commercial regarde une poussière placée sur le verre. Que voit-il ?
l'observateur regarde un défaut ponctuel de l'aluminure. Que voit-il ?
Solution

Nous avons représenté sur la figure ci-dessus l'image \(A'\) d'un point objet \(A\) donnée par un miroir plan se comportant tel qu'il est défini en optique géométrique. (1 pt)
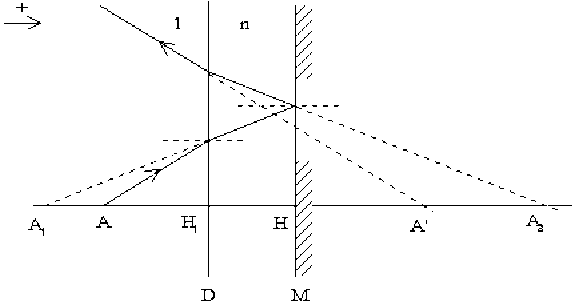
Représentons sur la figure ci-dessus le cas d'un miroir commercial : (1 pt)
Représentons l'obtention de l'image \(A'\) au travers des différents dioptres traversés :
\(A_1\) est l'image de \(A\) à travers le dioptre plan \(D\) de sommet \(H_1\) :
\(\overline{AH_1}=\frac{\overline{A_1H_1}}n\rightarrow\overline{A_1H_1}=n\overline{AH_1}\)
\(A_2\) est l'image de \(A_1\) à travers le miroir plan \(M\) de sommet \(H\) :
\(\overline{A_1H}=-\overline{A_2H}\rightarrow\overline{A_2H}=-\overline{A_1H}\)
\(A'\) est l'image de \(A_2\) à travers le dioptre plan \(D\) de sommet \(H_1\) :
\(\frac{\overline{A_2H_1}}n=\frac{\overline{A'H_1}}1\rightarrow\overline{A'H_1}=\frac1n\overline{A_2H_1}\)
\(\overline{A'H_1}=\frac1n(\overline{A_2H}+\overline{HH_1})=\frac1n(-\overline{A_1H}+\overline{HH_1})\)
\(=\frac1n(-\overline{A_1H_1}-\overline{H_1H}+\overline{HH_1})\)
\(=-\overline{AH_1}+2\frac{\overline{HH_1}}n\)
si \(e=\overline{H_1H}\) alors \(\overline{A'H_1}=-\overline{AH_1}-2\frac en\) (2 pts)
on cherche le miroir plan équivalent \(M\) tel que : \(\overline{AM}=-\overline{A'M}\) (symétrique) ; de \(\overline{A'H_1}=-\overline{AH_1}-2\frac en\)
on tire : \(\overline{A'M}+\overline{MH_1}=-\overline{AM}-\overline{MH_1}-2\frac en\)
\(2\overline{MH_1}=-2\frac en\) ; \(\overline{MH_1}=-\frac en\) (1) (1 pt)
un observateur placé devant un miroir commercial regarde une poussière placée sur le verre. Que voit-il ?
L'observateur voit la poussière et son image à travers le système optique. (1 pt)
l'observateur regarde un défaut ponctuel de l'aluminure. Que voit-il ?
\(\substack{{M_{i}}\\{(n)}}~\stackrel{D}{\substack{{\longrightarrow}\\{H_{1}}}}~\substack{{M_{1}}\\{(1)}}\) appliquons la relation de conjugaison concernant le dioptre \(D\) de sommet \(H_1\) : \(\frac{\overline{M_iH_1}}n=\frac{\overline{M_1H_1}}1\) soit encore : \(-\frac en=\overline{M_1H_1}=\overline{MH_1}\) d'après la relation (1) , donc \(M\) et \(M_1\) sont confondus et le défaut est vu sur le miroir équivalent. (2 pts)