Prismes accolés
Durée : 6 mn
Note maximale : 2
Question
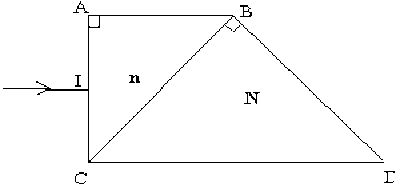
On considère un prisme rectangle isocèle \(ABC\), rectangle en \(A\), d'indice \(n=1,5\). On accole à ce prisme un autre prisme \(BCD\) rectangle en \(B\) d'indice \(N\). Un faisceau de rayons incidents arrive normalement à la face \(AC\) et subit une réfraction sur la face \(BC\).
Quelles conditions doivent satisfaire les indices \(n\) et \(N\) pour que ce faisceau émerge par la face CD après avoir subi une réflexion totale sur la face \(BD\) ?
Solution
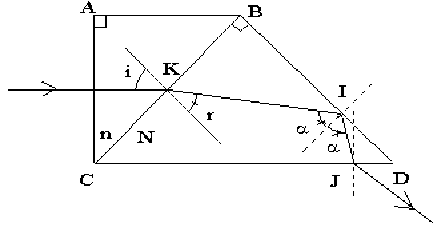
soit \(\lambda'\) l'angle de réfraction limite sur la face \(BD\). On a alors : \(N.\sin\lambda'=1\)
en \(K\) on écrira : \(n.\sin\frac{\pi}4=N\sin r\)
\(\alpha+r=\frac\pi2\) d'où \(n\frac{\sqrt2}2=N\sin\left(\frac{\pi}2-\alpha\right)=N\cos\alpha\)
or \(\sin\alpha=\sqrt{1-\cos^{2}\alpha}=\sqrt{1-\frac{n^2}{2N^2}}\) ; pour qu'il y ait réflexion totale en \(I\) il faut que :
\(\alpha>\lambda'\) soit : \(\sin\alpha>\sin\lambda'=\frac1N\) (1 pt)
\(\sqrt{1-\frac{n^2}{2N^2}}>\frac1N\) ou \(\sqrt{\frac{2N^2-n^2}{2N^2}}>\frac1N\) ou encore \(N^2-\frac{n^2}2>1\)
de plus \(\sin r\) doit être inférieur à 1 soit : \(\frac nN\frac{\sqrt2}2<1\)
\(\frac{n^2}{2N^2}<1\) ou \(n^2<2N^2\) ou encore \(N^2-\frac{n^2}2>0\)
cette deuxième condition sera vérifiée si la première l'est c'est-à-dire si : \(N^2-\frac{n^2}2>1\) (1 pt)