Prisme de verre
Durée : 10 mn
Note maximale : 6
Question
Un prisme de verre, d'indice \(n=1,5\) pour une radiation \(\lambda\), a pour section principale un triangle \(ABC,\)rectangle en \(B\) et d'angle \(c=15°\). Un rayon situé dans le plan de section principale pénètre la face \(AB\), se réfléchit totalement sur \(AC\) et émerge à travers \(BC\).
Quelles sont les valeurs des angles d'incidence, de réfraction et de réflexion ?
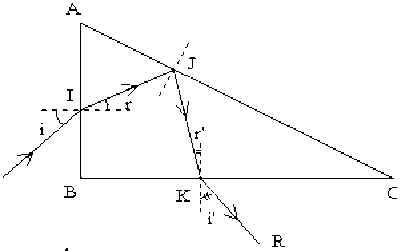
Solution
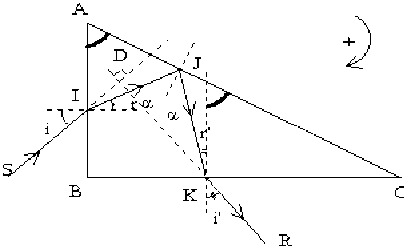
si \(SI\) est perpendiculaire à \(KR\) alors : \(D=\frac{\pi}2\)
\(D=(i-r)+(\pi-2\alpha)-(i'-r)\)
\(\frac{\pi}2=\pi+(i-i')-(r-r')-2\alpha\)
\(\frac{\pi}2=i'-i+r-r'+2\alpha\)
or \(r+\alpha=A\) et \(\left(\frac{\pi}2-\alpha\right)+r'=A\)
\(r-r'+2\alpha=\frac{\pi}2\)
d'où \(i' - i = 0 \rightarrow i' = i \rightarrow r = r'\) et \(\alpha=\frac{\pi}4\) or \(A=\frac{\pi}2-15°=75°\)
d'où \(r=A-\alpha=75°-45°=30°\)
\(\sin i' = \sin i = n . \sin r = 1,5 . ~0,5 = 0,75\) d'où : \(i = i' = 48,59° = 48°35'\) (2 pts)
le prisme restant fixe, le rayon incident tourne d'un angle a très petit. Quelle est la rotation correspondante du rayon émergent ?
Si \(i\) varie de \(di\) alors \(r\) varie de \(dr\) et \(\alpha\) varie de \(-d\alpha\) car
\(\alpha+r=A\rightarrow d\alpha+dr=0\) et comme
\(A=\left(\frac{\pi}2-\alpha\right)+r'\rightarrow dr'=d\alpha\) ainsi : \(\alpha\) varie de \(-d\alpha\)
\(dr'\) varie de \(-d\alpha\) et par suite \(i'\) varie de -\(di'\) ; ainsi quand \(i\) varie de \(+di\), \(i'\) varie de \(-di'\). (2 pts)
on se replace dans les conditions définies en 1) mais on utilise cette fois une lumière pour laquelle l'indice est \(n=n+dn (dn>0)\). De combien et dans quel sens tourne le rayon émergent ? (A.N : \(dn=0,002\)).
En \(I\) on a : \(\sin i = n . \sin r\) . Si l'on travaille à \(i\) constant alors
\(\sin r . dn + n . \cos r . dr = 0\) soit : \(dr=-\tan r\frac{dn}n\)
comme \(r+\alpha=A\) et \(A=\left(\frac{\pi}2-\alpha\right)+r'\), \(d\alpha=-dr\),
\(dr'=d\alpha=-dr=\frac{dn}n\tan r\)
en \(K\) on peut écrire : \(\sin i' = n \sin r'\) soit en différentiant :
\(\cos i' . di' = n . \cos r' . dr' + \sin r' . dn= \cos r' . dn . \tan r + \sin r' . dn = ( \cos r' . \tan r + \sin r' ) dn\)
or \(r = r'\) donc : \(\cos i' . di' = 2 \sin r . dn\)
soit : \(di'=2\frac{\sin r}{\cos i'}dn=2\frac{\sin r}{\cos i}dn\) (puisque \(i=i'\))
\(di'=2\tan i\frac{dn}n\) or ici \(i\le\frac{\pi}2\)
donc \(di'\) a le même signe que \(dn\). Soit ici \(di'>0\) et le rayon émergent tourne donc de façon que \(i'\) croisse de \(+di\). (2 pts)