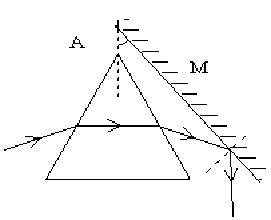
Prisme équilatéral et miroir
Durée : 10 mn
Note maximale : 4
Question
Un prisme équilatéral est lié de façon rigide à un miroir plan, parallèle à l'arête du prisme. Le prisme est utilisé au minimum de déviation.
déterminer la position du miroir pour que la déviation totale \(D\) ait une valeur prédéterminée. Cette position dépend-elle de l'angle \(A\) du prisme? A.N : \(D=0\) ; \(D=90°\).
les rayons émergents sont reçus par une cellule photoélectrique fixe. Pour explorer le spectre il faut donc tourner l'ensemble prisme + miroir. Dans le cas où \(D=90°\), calculer l'angle de rotation nécessaire pour passer de la raie \(\lambda=0,577\mu m\) à la raie \(\lambda'=0,579\mu m\) sachant que l'indice du prisme est donné par : \(n=1,5500+\frac a{\lambda^2}\) avec \(a=2.10^{-4}U.S.I\)
Pratiquement, le système prisme + miroir est remplacé par un prisme \(LMN\) rectangle en \(M\), dont l'hypoténuse joue le rôle de miroir. En conservant toujours \(D=90°\) et \(i=i_m\), montrer que ce dispositif est réalisable et calculer les angle \(L\) et \(N\) du prisme.
Solution
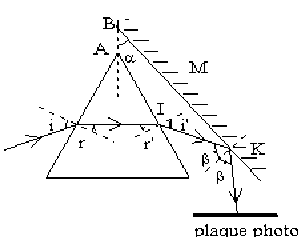
déterminer la position du miroir pour que la déviation totale \(D\) ait une valeur prédéterminée. Cette position dépend-elle de l'angle \(A\) du prisme ? A.N : \(D=0\) ; \(D=90°\).
\(D=(i-r)+(i'-r')+\pi-2\beta\) or au minimum de déviation : \(i=i'=i_m\)
comme \(r + r' = A\) on en déduit : \(D=2i_m-A+\pi-2\beta\). Considérons le quadrilatère \(BKIA\) :
\(\alpha+\left(\pi-\frac A2\right)+\left(\frac{\pi}2+i_m\right)+\left(\frac{\pi}2-\beta\right)\)
\(\beta=\alpha-\frac A2+i_m\)
et \(D=2i_m-A+\pi-2\alpha+A-2i_m\)
soit \(D=\pi-2\alpha\) déviation qui est indépendante de \(A\).
si \(D=0\rightarrow\alpha=\frac{\pi}2\) ce qui est impossible
si \(D=\frac{\pi}2\rightarrow\alpha=\frac{\pi}4\) ce qui est possible physiquement. (2 pts)
Dans le cas où \(D=90°\), calculer l'angle de rotation nécessaire pour passer de la raie \(\lambda =0,577\mu\) m à la raie \(\lambda'=0,579\mu m\) . Calculer les angle \(L\) et \(N\) du prisme.
à l'entrée du prisme : \(\sin i = n . \sin r\) avec \(r + r' = A\) . Au minimum de déviation on pourra écrire :
\(\sin i_m=n.\sin\frac A2=n.\frac{1}2\) (prisme équilatéral \(\rightarrow A=60°\)) or \(n=k+\frac a{\lambda^2}\)
d'où \(\cos i_m.di_m=-\frac a{\lambda^3}d\lambda\) soit : \(\Delta i_m=\frac a{\lambda^3\cos i_m}\Delta\lambda\) et enfin :
\(\Delta i_m=\frac a{\lambda^3\sqrt{1-\frac{n^2}4}}\Delta\lambda\)
l'application numérique conduit à : \(D i_m=1'12''\). (2 pts)