Réfractomètre
Durée : 10 mn
Note maximale : 4
Question
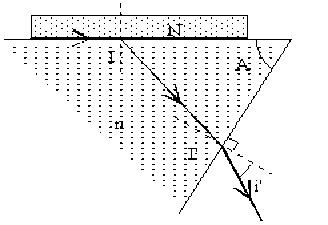
Réfractomètre de Pulfrich et réfractomètre d'Abbe. Un rayon lumineux provenant d'un milieu d'indice \(N\) inconnu, tombe à incidence rasante sur un prisme d'angle \(A\). Il émerge du prisme en faisant un angle \(i'\) avec la normale à la face de sortie du prisme.
Calculer \(N\) dans les deux cas suivants :
cas du réfractomètre de Pulfrich où \(n=1,732\) ; \(A=90°\) et \(i'=30°\)
cas du réfractomètre d'Abbe où \(n=1,6\) ; \(A=61°\) et \(i'=15°\)
Solution
appliquons les relations de Snell-Descartes à l'entrée et à la sortie du prisme d'angle \(A\) : \(N . \sin i = n . \sin r\) (1)
\(r + r' = A\) (2)
\(n . \sin r' = \sin i'\) (3)
(1) → \(N = n . \sin r\)
(2) et (3) → \(\sin i' = n . \sin (A-r)\)
\(= n . \sin A . \cos r - n . \sin r . \cos A = n . \sin A . \cos r - N . \cos A\)
soit encore :
\(\sin i'=n.\sin A\sqrt{1-\frac{N^2}{n^2}}-N.\cos A\)
\(\sin i'+N.\cos A=n.\sin A\sqrt{1-\frac{N^2}{n^2}}\)
\((\sin i'+N.\cos A)^2=n^2.\sin^2A\left(1-\frac{N^2}{n^2}\right)\)
\(sin^2i'+N^2cos^2A+2N\sin i'\cos A=n^2\sin^2A-N^2\sin^2A\)
\(N^2+2N\sin i'\cos A+(sin^2i'-n^2\sin^2A)=0\)
on aboutit alors à une équation du second degré en \(N\) (2 pts)
Considérons le cas du réfractomètre de Pulfrich où : \(n=1,732\), \(A=90°\),
\(i'=30°\) ; alors \(\cos A=0\) et l'équation se réduit à :
\(N^2+(0,5^2-3)=0\rightarrow N=1,66\) (1 pt)
Considérons le cas du réfractomètre d'Abbe où : \(n=1,6\), \(A=61°\),
\(i'=15° ;\)
alors \(2.\sin i'.\cos A= 2 .0,258.0,484 = 0,251\)
\((\sin^2i'-n^2\sin^2A)=0,258^2-1,6^2.0,874^2=1,891\)
l'équation devient : \(N^2+0,251.N-1,891=0\) dont la seule solution possible est après résolution : \(N=1,255\) (1 pt)