Centre optique
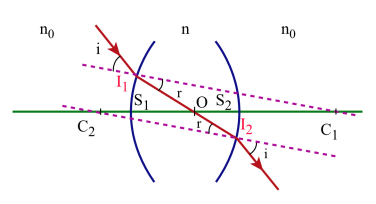
Le centre optique[1] O d'une lentille est un point de l'axe, appartenant au milieu réfringent n, qui peut être intérieur ou extérieur au segment S1S2,et tel qu'à tout rayon se propageant dans la lentille et passant par ce point correspondent un rayon incident et un rayon émergent parallèles.
On mène par C1 et C2 deux parallèles qui coupent les dioptres sphériques en I1 et I2 : les angles C1I1I2 et C2I2I1 sont égaux à r. C1I1 est également la normale en I1 au dioptre sphérique et si i est l'angle d'incidence on peut écrire: no . sin i = n . sin r
C2I2 est de la même façon une normale au dioptre de sortie en I2 et si i' est l'angle d'émergence on pourra écrire la relation: no . sin i' = n . sin r
on en déduit donc puisque les milieux extrêmes sont identiques que : i = i'.
Le point O, point d'intersection de I1I2 avec l'axe optique, correspond bien à la définition du centre optique. Si on considère les plans tangents aux dioptres en I1 et I2, cela signifie que pour les rayons qui passent par O, le système épais se comporte comme une lame à faces parallèles et donc les plans tangents sont des plans parallèles entre eux.
Considérons les triangles OC1I1 et OC2I2 on a :
\(\frac{\overline{\mathrm{OC}_1}}{\overline{\mathrm{OC}_2}}=\frac{\overline{\mathrm C_1\mathrm I_1}}{\overline{\mathrm C_2\mathrm I_2}}=\frac{\overline{\mathrm S_1\mathrm C_1}}{\overline{\mathrm S_2\mathrm C_2}}=\frac{\overline{\mathrm{OC}_1}~-~\overline{\mathrm S_1\mathrm C_1}}{\overline{\mathrm{OC}_2}~-~\overline{\mathrm S_2\mathrm C_2}}=\frac{\overline{\mathrm{OS}_1}}{\overline{\mathrm{OS}_2}}=\frac{\mathrm R_1}{\mathrm R_2}\)
Le point O divise le segment S1S2 dans le rapport des valeurs algébriques des rayons de courbure et est donc unique. Il ne dépend pas de la valeur de l'indice du verre constituant la lentille épaisse. O est situé entre S1 et S2 si R1 et R2 sont de signes contraires, O est extérieur à S1S2 si R1 et R2 sont de même signe; O est toujours plus proche de la face la plus courbe.
De la relation précédente on déduit :
\(\frac{\overline{\mathrm S_2\mathrm C_2}}{\overline{\mathrm S_1\mathrm C_1}}=\frac{\overline{\mathrm{OS}_2}}{\overline{\mathrm{OS}_1}}=\frac{\overline{\mathrm{OS}_1}~+~\overline{\mathrm S_1\mathrm S_2}}{\overline{\mathrm{OS}_1}}=1+\frac{\overline{\mathrm S_1\mathrm S_2}}{\overline{\mathrm{OS}_1}}\)
d'où :
\(\overline{\mathrm S_1\mathrm O}=\frac{\overline{\mathrm S_1\mathrm C_1}}{\overline{\mathrm S_1\mathrm C_1}~-~\overline{\mathrm S_2\mathrm C_2}}~\overline{\mathrm S_1\mathrm S_2}\)
\(\overline{\mathrm S_2\mathrm O}=\frac{\overline{\mathrm S_2\mathrm C_2}}{\overline{\mathrm S_1\mathrm C_1}~-~\overline{\mathrm S_2\mathrm C_2}}~\overline{\mathrm S_1\mathrm S_2}\)