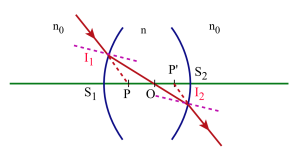
Plans principaux
Introduction
Les milieux extrêmes étant identiques les points principaux P et P' seront confondus avec les points nodaux N et N'. (voir systèmes centrés)
Les points principaux P et P' étant confondus avec les points nodaux N et N' on pourra dire que le centre optique[1] O est le conjugué de P dans le premier dioptre tandis que le point P' sera le conjugué de O dans le second dioptre.
En écrivant les relations de conjugaison correspondantes pour chacun des dioptres :
\(\frac{\mathrm n_0}{\overline{\mathrm S_1\mathrm P}}-\frac{\mathrm n}{\overline{\mathrm S_1\mathrm O}}=\frac{\mathrm n_0-\mathrm n}{\overline{\mathrm S_1\mathrm C_1}}\)
\(\frac{\mathrm n}{\overline{\mathrm S_2\mathrm O}}-\frac{\mathrm n_0}{\overline{\mathrm S_2\mathrm{P'}}}=\frac{\mathrm n-\mathrm n_0}{\overline{\mathrm S_2\mathrm C_2}}\)
en développant la première relation et en remplaçant S1O par sa valeur :
\(\frac{\mathrm n_0}{\overline{\mathrm S_1\mathrm P}}-\frac{\mathrm n~\Big(\overline{\mathrm S_1\mathrm C_1}~-~\overline{\mathrm S_2\mathrm C_2}\Big)}{\overline{\mathrm S_1\mathrm C_1}~\overline{\mathrm S_1\mathrm S_2}}=\frac{\mathrm n_0-\mathrm n}{\overline{\mathrm S_1\mathrm C_1}}\)
\(\frac{\mathrm n_0}{\overline{\mathrm S_1\mathrm P}}=\frac{\Big(\mathrm n_0~-~\mathrm n\Big)~\overline{\mathrm S_1\mathrm S_2}~+~\mathrm n~\Big(\overline{\mathrm S_1\mathrm C_1}~-~\overline{\mathrm S_2\mathrm C_2}\Big)}{\overline{\mathrm S_1\mathrm C_1}~\overline{\mathrm S_1\mathrm S_2}}\)
\(\overline{\mathrm S_1\mathrm P}=\frac{\mathrm n_0~\overline{\mathrm S_1\mathrm C_1}~\overline{\mathrm S_1\mathrm S_2}}{\Big(\mathrm n_0~-~\mathrm n\Big)~\overline{\mathrm S_1\mathrm S_2}~+~\mathrm n~\Big(\overline{\mathrm S_1\mathrm C_1}~-~\overline{\mathrm S_2\mathrm C_2}\Big)}\)
de même :
\(\overline{\mathrm S_2\mathrm{P'}}=\frac{\mathrm n_0~\overline{\mathrm S_2\mathrm C_2}~\overline{\mathrm S_1\mathrm S_2}}{\Big(\mathrm n_0~-~\mathrm n\Big)~\overline{\mathrm S_1\mathrm S_2}~+~\mathrm n~\Big(\overline{\mathrm S_1\mathrm C_1}~-~\overline{\mathrm S_2\mathrm C_2}\Big)}\)
et en fonction de C1C2 :
\(\overline{\mathrm S_1\mathrm P}=\frac{\mathrm n_0~\overline{\mathrm S_1\mathrm C_1}~\overline{\mathrm S_1\mathrm S_2}}{\Big(\mathrm n_0~-~\mathrm n\Big)~\overline{\mathrm S_1\mathrm S_2}~+~\mathrm n~\Big(\overline{\mathrm S_1\mathrm S_2}~+~\overline{\mathrm S_2\mathrm C_1}~-~\overline{\mathrm S_2\mathrm C_2}\Big)}\)
\(=\frac{\mathrm n_0~\overline{\mathrm S_1\mathrm C_1}~\overline{\mathrm S_1\mathrm S_2}}{\Big(\mathrm n_0~-~\mathrm n\Big)~\overline{\mathrm S_1\mathrm S_2}~+~\mathrm n~\Big(\overline{\mathrm S_1\mathrm S_2}~+~\overline{\mathrm C_2\mathrm C_1}\Big)}\)
\(\overline{\mathrm S_1\mathrm P}=\frac{\mathrm n_0~\overline{\mathrm S_1\mathrm C_1}~\overline{\mathrm S_1\mathrm S_2}}{\mathrm n_0~\overline{\mathrm S_1\mathrm S_2}~+~\mathrm n~\overline{\mathrm C_2\mathrm C_1}}\)
\(\overline{\mathrm S_2\mathrm{P'}}=\frac{\mathrm n_0~\overline{\mathrm S_2\mathrm C_2}~\overline{\mathrm S_1\mathrm S_2}}{\mathrm n_0~\overline{\mathrm S_1\mathrm S_2}~+~\mathrm n~\overline{\mathrm C_2\mathrm C_1}}\)
On peut alors définir l'interstice de la lentille par la valeur algébrique de la distance entre les points principaux objet et image :
\(\overline{\mathrm P\mathrm{P'}}=\frac{\overline{\mathrm S_1\mathrm S_2}~\overline{\mathrm C_1\mathrm C_2}~\bigg(1~-~\frac{\mathrm n}{\mathrm n_0}\bigg)}{\overline{\mathrm S_1\mathrm S_2}~-~\frac{\mathrm n}{\mathrm n_0}~\overline{\mathrm C_1\mathrm C_2}}\)