Définir le dioptre unique équivalent de l'œil au repos [L'oeil et la vision]

Définir le dioptre unique équivalent de l'œil au repos

Durée : 6 mn

Note maximale : 10

Question

On peut établir que l'oeil au repos est un système centré dont les points principaux (H et H') espacés de 0,3 mm sont situés 2 mm en arrière du sommet de la cornée, et dont les points nodaux (N et N') espacés de 0,3 mm sont situées 6 mm en arrière des points principaux. Les distances focales de ce système sont -17 et +23 mm.

Vérifier que l'oeil emmétrope au repos peut être schématisé par un dioptre unique séparant l'air d'un milieu d'indice n' = 1,353 dont on calculera la distance focale. Préciser les positions, relatives aux éléments de l'œil ci-dessous, du foyer image F',du sommet S_e et du centre C de ce dioptre équivalent.

Solution

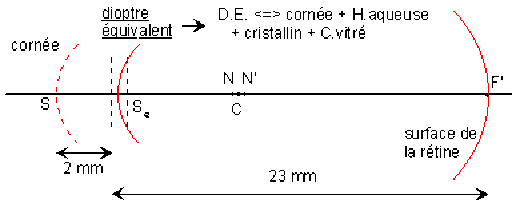
(3 pts)

On admet que \(\overline{HH'}=\overline{NN'}=\textrm{0,3 mm}\) sont assez petit devant f '=23 mm pour poser

\(\overline{HH'}=\overline{NN'}=\textrm{0,3 mm}\) (2 pts). Pour que l'œil emmétrope au repos soit assimilable à un dioptre unique, il faut que le sommet S_e de ce dioptre soit en M, milieu des points H et H', son centre en C milieu des points nodaux N et N' et son foyer image F' sur la rétine soit :

\(S_eF'=f'_e=\frac{n'}{n'-n}.\overline{S_eC}=\frac{\textrm{1,353}}{\textrm{0,353}}.(6)=\textrm{22,997 mm}\) (3pts)

\(S_eF'=f'_e=\frac{n'}{n'-n}.\overline{S_eC}=\textrm{23 mm}\) CQFD (2pts)

(on vérifie ainsi que le foyer image du dioptre sphérique équivalent de l'œil est sur la rétine)