Calculer et comparer deux amplitudes d'accommodation [L'oeil et la vision]

Calculer et comparer deux amplitudes d'accommodation

Durée : 6 mn

Note maximale : 12

Question

Calculer les puissances d'accommodation Δ P (désignées aussi par A) des sujets ci-après :

	sujet 1	sujet 2
distance minimum de vision distincte d_m ou d, en m	1	0,1
distance maximum de vision distincte d_M ou d, en m	\(\infty\)	\(\infty\)

Quel est le sujet le plus âgé ?

On assimilera la puissance d'accommodation \(\Delta P\) (due au cristallin) à celle d'une lentille mince qui accolée à l'œil normal au repos lui permettrait sans accommodation de voir nettement un objet situé à la distance minimum de vision distincte, d_m.

Solution

L'amplitude (ou puissance) d'accommodation est égale à à la puissance de la lentille mince qui effectuerait ce travail d'accommodation tout en laissant l'œil au repos. Une telle lentille doit donner d'un objet A situé au proximum une image A' à l'infini, parfaitement visible par l'œil au repos.

\(\frac{-1}{\overline{SA}}+\frac{1}{\overline{SA'}}=\frac{1}{f'}=\frac{-1}{p}+\frac{1}{p'} \quad \overline{SA}=p=-d_m \quad \overline{SA'}=p'=-\infty\) et \(\Delta P=P_{\textrm{lent}}=\frac{1}{f'}\) (4 pts)

Sujet 1 : \(p=- \textrm{1 m}\) et \(p'=-\infty, \Delta P=1=1~D\) (2 pts)

Sujet 1 : \(p=-\textrm{0,1 m}\) et \(p'=-\infty, \Delta P=\frac{1}{\textrm{0,1}}=10~D\) (2 pts)

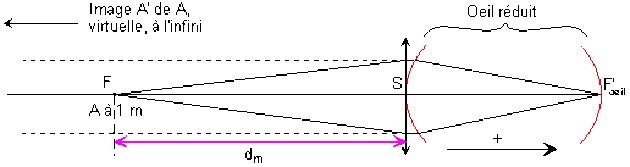
L'amplitude d'accommodation diminue avec l'âge et il en résulte un éloignement du proximum avec l'âge. Le sujet le plus âgé est celui dont le proximum est à un mètre (2 pts).