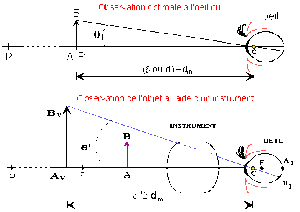
Grossissement réel minimum
Durée : 6 mn
Note maximale : 8
Question
Trouver la condition nécessaire pour que le grossissement réel minimum procuré à l'observateur par un instrument d'observation rapprochée (loupe, microscope, ...) soit indépendant de la position de cet observateur derrière l'instrument.
Comment appelle-t-on ce grossissement ?
On suppose établie la formule du grossissement réel : \(G=\frac{\delta}{f'}\left(1-\frac{\overline{F'C}}{\delta'}\right)\)
f '=distance focale image de l'instrument.
F'=foyer image de l'instrument.
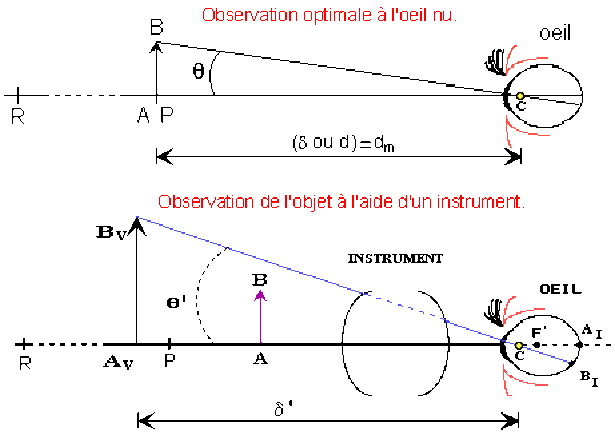
Solution
Le grossissement réel \(G=\frac{q'}{q}\) est minimum lorsque q est maximum, c'est-à -dire lorsque d=dm. Lorsque l'observateur se déplace, la distance \(\overline{F'C}\) entre le centre optique de l'œil et le foyer image f ' varie, mais \(\overline{F'C}/\delta'\) tend vers 0 dès que l'observateur règle l'oculaire pour avoir une image virtuelle AVBV de l'objet AB à l'infini :
\(\delta'=A_VC\rightarrow\infty\Rightarrow\frac{\overline{F'C}}{\delta'}\rightarrow0\)
L'objet est placé dans le plan focal objet de l'instrument, l'image fournie par l'instrument est rejetée à l'infini (2 pts) et le grossissement \(G=\frac{\theta'}{\theta}=\frac{\delta}{f'}\left(1-\frac{\overline{F'C}}{\delta'}\right)=\frac{\delta}{f'}\) (2 pts) ne dépend plus que de la distance d de l'objet à l'œil dans l'observation à l'oeil nu (2 pts). G ne peut être inférieur à \(\frac{d_m}{f'}\).
Ce grossissement réel particulier, indépendant de la position de l'observateur par rapport l'instrument, s'appelle grossissement intrinsèque (2 pts). Il n'a pas de valeur numérique calculable puisqu'il dépend de d.