Latitude de mise au point
Durée : 6 mn
Note maximale : 10
Question
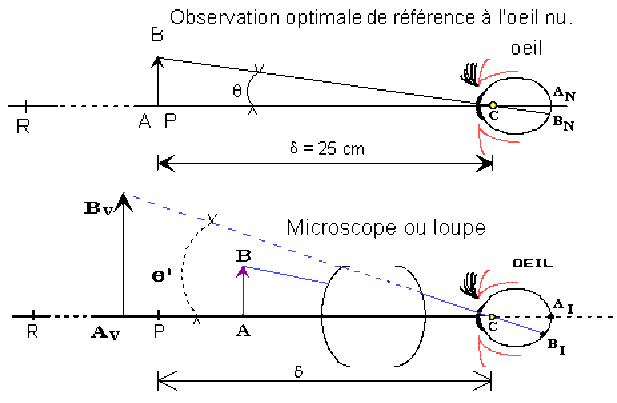
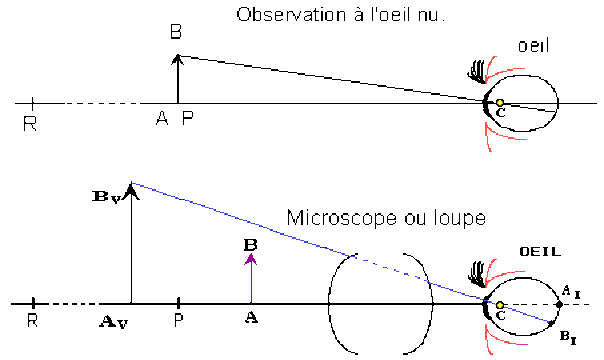
Justifier la nécessité et la signification pratique du grossissement commercial du microscope en complétant les schémas ci-dessous.
Solution
Le diamètre apparent q d'un petit objet, dans l'observation à l'oeil nu est défini par
\(\theta=\hat{ACB}~\#~\tan(\hat{ACB}) = AB / \delta\). Si \(\theta'\) est le diamètre apparent de l'image de l'objet vue à travers l'instrument, le grossissement est : \(G =\frac{\theta'}{\theta}\).
Dans l'observation de petits objets, la distance du centre optique de l'oeil à l'objet peut varier pour un même observateur selon les conditions matérielles d'observation. Elles peuvent également varier d'un observateur à l'autre (3 pts). Un paramètre qui se veut caractéristique d'un instrument ne peut être défini par une variable. Cette ambigüité est levée par une convention qui fixe arbitrairement à 0,25 m la valeur de confort de la distance minimum d'observation à l'oeil nu. Cette convention à le second avantage de définir le grossissement minimum qui sera obtenu avec la loupe ou le microscope lorsque l'observateur emmétrope règle l'instrument pour obtenir une image à l'infini.
Le grossissement \(G_0=\frac{\theta'}{\theta}=\frac{\textrm{0,25}}{f'}\) ainsi obtenu est appelé grossissement commercial (5 pts). La distance de 0,25 m est également celle qui permet le plus grand diamètre apparent de l'objet sans fatigue excessive pour un œil emmétrope (2 pts).