Définitions
Le produit vectoriel de deux vecteurs \(\overrightarrow{U}\) et \(\overrightarrow{V}\), est un vecteur \(\overrightarrow{W}\), noté \(\overrightarrow{W} = \overrightarrow{U} \wedge \overrightarrow{V}\) de :
direction : \(\overrightarrow{W} \perp \overrightarrow{U}\) et \(\overrightarrow{W} \perp \overrightarrow{V}\)
sens : trièdre \(\Big(\overrightarrow{U},\overrightarrow{V},\overrightarrow{W} \Big)\) direct
norme : \(\Big\Arrowvert \overrightarrow{W} \Big\Arrowvert = \Big\Arrowvert \overrightarrow{U} \Big\Arrowvert ~\Big\Arrowvert \overrightarrow{V} \Big\Arrowvert ~\Big\arrowvert \sin \Big(\overrightarrow{U}, \overrightarrow{V}\Big)\Big\arrowvert\)
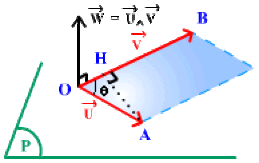
\(\Big\Arrowvert \overrightarrow{W} \Big\Arrowvert\) est l'aire du parallélogramme construit sur les représentants \(\overrightarrow{OA}\) et \(\overrightarrow{OB}\) des vecteurs \(\overrightarrow{U}\) et \(\overrightarrow{V}\). En effet, \(AH = OA \sin \theta =\Big\Arrowvert \overrightarrow{U} \Big\Arrowvert ~\Big\arrowvert \sin \Big(\overrightarrow{U}, \overrightarrow{V}\Big)\Big\arrowvert\) et l'aire du parallélogramme devient :
\(OB \times AH = \Big\Arrowvert \overrightarrow{V} \Big\Arrowvert ~\Big\Arrowvert \overrightarrow{U} \Big\Arrowvert ~\Big\arrowvert \sin \Big(\overrightarrow{U}, \overrightarrow{V}\Big)\Big\arrowvert\).
En posant \(U_x , U_y , U_z\) et \(V_x , V_y , V_z\) les composantes respectives de \(\overrightarrow{U}\) et \(\overrightarrow{V}\) dans la base orthonormée \(\Big(\vec{i},\vec{j},\vec{k} \Big)\), le produit vectoriel de ces deux vecteurs est le vecteur défini par la relation :
\(\overrightarrow{W} = \overrightarrow{U} \wedge \overrightarrow{V} = \Big(U_{y}V_{z} - U_{z}V_{y}\Big) \vec{i} + \Big(U_{z}V_{x} - U_{x}V_{z}\Big)\vec{j} + (U_{x}V_{y} - U_{y}V_{x} \Big) \vec{k}\)
sachant que :
\(\vec{i} \wedge \vec{j} = \vec{k} ~;~ \vec{j} \wedge \vec{k} = \vec{i} ~;~ \vec{k} \wedge \vec{i} = \vec{j}\)
\(\vec{i} \wedge \vec{i} = \vec{j} \wedge \vec{j} = \vec{k} \wedge \vec{k} = \vec{0}\)
Disposition pratique :
\(\overrightarrow{U} \wedge \overrightarrow{V} = \left[ \begin{array}{c} U_{x} \\ U_{y} \\ U_{z} \end{array} \right. \wedge \left[ \begin{array}{c} V_{x} \\ V_{y} \\ V_{z} \end{array} \right. = \left[ \begin{array}{c} U_{y}V_{z} - U_{z}V_{y }\\ U_{z}V_{x} - U_{x}V_{z } \\ U_{x}V_{y} - U_{y}V_{x } \end{array} \right.\)
Pour obtenir les composantes du produit vectoriel :
1. Ajouter dans chacune des colonnes des composantes de \(\overrightarrow{U}\) et de \(\overrightarrow{V}\) les composantes sur \(\vec{i}\) et \(\vec{j}\).
2. Effectuer la différence des "produits en croix"