Applications
En géométrie (dans un repère orthonormé)
Mesure de l'aire d'un parallélogramme \(ABCD\) ou d'un triangle \(ABC\)
Aire du parallélogramme \((ABCD) =\Big\Arrowvert \overrightarrow{AB} \wedge \overrightarrow{AD}\Big\Arrowvert\)
Aire du triangle \((ABC) = \frac{1}{2} \Big\Arrowvert \overrightarrow{AB} \wedge \overrightarrow{AD}\Big\Arrowvert\)
Exemple : Calcul de l'aire d'un triangle
Dans le plan \(xOy\), nous avons les trois points \(A(2,1) ~;~ B(-1,0)~ ;~ C(3,-4)\).
Calculer l'aire \(S\) du triangle \(ABC\).
Par définition \(S = \frac{1}{2} \Big\Arrowvert \overrightarrow{AB} \wedge \overrightarrow{AC}\Big\Arrowvert\)
avec \(\overrightarrow{AB} = \overrightarrow{OB} - \overrightarrow{OA} = (-3,1)\)
et \(\overrightarrow{AC} = \overrightarrow{OC} - \overrightarrow{OA} = (1,-5)\)
d'où
\(\overrightarrow{AB} \wedge \overrightarrow{AC} = \left[\begin{array}{c} -3 \\ -1 \end{array} \right. \wedge \left[\begin{array}{c} 1 \\ -5 \end{array} \right. = 15 + 1 = 16 \vec{k}\)
(composante sur \((Oz)\))
\(S = \frac{1}{2} \Big\Arrowvert \overrightarrow{AB} \wedge \overrightarrow{AC}\Big\Arrowvert = 8 \textrm{ ua}\)
Equation cartésienne d'une droite \((D)\) passant par deux points \(A\) et \(B\) d'un plan \(xOy\).
Si un point \(M \in (D)\) alors \(\overrightarrow{AM} \wedge \overrightarrow{AB} = \overrightarrow{0}\)
Exemple : Détermination de l'équation cartésienne d'une droite
A partir du produit vectoriel, retrouver l'équation cartésienne de la droite \((D)\) qui passe par les points \(A(2,-1)\) et \(B(1,2)\) du plan \(xOy\) rapporté à un repère orthonormé.
Si un point \(M(x,y) \in (D)\) alors : \(\overrightarrow{AM} \wedge \overrightarrow{AB} = \overrightarrow{0}\), comme
\(\overrightarrow{AM} = \overrightarrow{OM} - \overrightarrow{OA} = \left[\begin{array}{c} x \\ y \end{array} \right. - \left[\begin{array}{c} 2 \\ -1 \end{array} \right. = \left[\begin{array}{c} x-2 \\ y+1 \end{array} \right.\)
\(\overrightarrow{AB} = \overrightarrow{OB} - \overrightarrow{OA} = \left[\begin{array}{c} 1 \\ 2 \end{array} \right. - \left[\begin{array}{c} 2 \\ -1 \end{array} \right. = \left[\begin{array}{c} -1 \\ 3 \end{array} \right.\)
d'où
\(\overrightarrow{AM} \wedge \overrightarrow{AB} =\overrightarrow{0} \Leftrightarrow \left[\begin{array}{c} (x-2) \\ (y+1) \end{array} \right. \wedge \left[\begin{array}{c} -1 \\ 3 \end{array} \right. = [3(x-2) + (y+1)]\vec{k} = \overrightarrow{0}\)
donc \(3(x-2) + y + 1 = 0\)
\(\Rightarrow\) \(3x + y - 5 = 0\) Equation cartésienne de la droite \((D)\)
En Physique
Moment d'un vecteur par rapport à un point
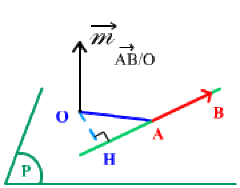
Moment de vecteur \(\overrightarrow{AB}\) par rapport au point \(O\) est le vecteur :
\(\overrightarrow{m} ~\overrightarrow{AB}/o = \overrightarrow{OA} \wedge \overrightarrow{AB}\)
Module : \(\Big\Arrowvert \overrightarrow{m} ~\overrightarrow{AB}/o\Big\Arrowvert = \Big\Arrowvert \overrightarrow{OA} \wedge \overrightarrow{AB} \Big\Arrowvert = \Big\Arrowvert \overrightarrow{OA} \Big\Arrowvert \Big\Arrowvert \overrightarrow{AB} \Big\Arrowvert \sin \Big(\overrightarrow{OA},\overrightarrow{AB}\Big)\)
avec \(OH = \Big\Arrowvert \overrightarrow{OA} \Big\Arrowvert \sin \Big(\overrightarrow{OA},\overrightarrow{AB}\Big)\)
\(\qquad\)
Force subie par une charge ponctuelle \(q\) se déplaçant à la vitesse \(\overrightarrow{v}\) dans un champ magnétique uniforme \(\overrightarrow{B}\):
\(\overrightarrow{F} = q ~\overrightarrow{v} \wedge \overrightarrow{B}\) \(\quad\) (Force de Lorentz)