Applications
En géométrie
Détermination du volume d'un parallélépipède connaissant les arêtes \(\overrightarrow{OA}\) , \(\overrightarrow{OB}\) et \(\overrightarrow{OC}\):
\(V = \Big\arrowvert \Big(\overrightarrow{OA},\overrightarrow{OB},\overrightarrow{OC}\Big)\Big\arrowvert\)
Exemple : Volume d'un parallélépipède
Détermination du volume du parallélépipède construit sur les arêtes \(\overrightarrow{OA}\Big(3,6,3 \Big)\);
\(\overrightarrow{OB}\Big(1,3,-2\Big)\) et \(\overrightarrow{OC}\Big(2,2,2 \Big)\).
\(V = \Big\arrowvert \Big(\overrightarrow{OA},\overrightarrow{OB},\overrightarrow{OC}\Big)\Big\arrowvert = \Big\arrowvert \Big(\overrightarrow{OA}\wedge\overrightarrow{OB}\Big)\cdot\overrightarrow{OC}\Big\arrowvert\)
avec \(\overrightarrow{OA}\wedge\overrightarrow{OB} = \left[ \begin{array}{c} 3 \\ 6 \\ 3 \end{array} \right. \wedge \left[ \begin{array}{c} 1 \\ 3 \\ -2 \end{array} \right. = \left[ \begin{array}{c} -12 - 9 = -21\\ -(-6-3) = 9\\ 9-6 = 3\end{array} \right.\)
et \(\Big(\overrightarrow{OA}\wedge\overrightarrow{OB}\Big) \cdot \overrightarrow{OC} = \left[ \begin{array}{c} -21 \\ 9 \\ 3 \end{array} \right. \cdot \left[ \begin{array}{c} 2 \\ 2 \\ 2 \end{array} \right. = -(21)(2) + (9)(2) + (3)(2) = -18\)
et volume du parallélépipède :
\(V = \Big\arrowvert \Big(\overrightarrow{OA},\overrightarrow{OB},\overrightarrow{OC}\Big)\Big\arrowvert = \Big\arrowvert -18 \Big\arrowvert = 18 \textrm{ uv}\)
\(\qquad\)
Equation cartésienne d'un plan \((P)\) passant par trois points \(A\), \(B\) et \(C\).
Si \(M \in \Big(P\Big)\) alors : \(\Big(\overrightarrow{AB},\overrightarrow{AC},\overrightarrow{AM}\Big) = 0\)
Exemple : Equation d'un plan
Equation cartésienne du plan \((P)\) passant par les points : \(A (1,7,1)\) ; \(B(3,4,1)\) et
\(C (-1,-2,5)\) rapportés à un repère orthonormé.
Si un point \(M(x,y,z) \in \Big(P\Big)\) alors : \(\Big(\overrightarrow{AB}\wedge\overrightarrow{AC}\Big) \cdot \overrightarrow{AM} = 0\)
\(\overrightarrow{AB} = \overrightarrow{OB} - \overrightarrow{OA} = \left[ \begin{array}{c} 3 \\ 4 \\ 1 \end{array} \right. - \left[ \begin{array}{c} 1 \\ 7 \\ 1 \end{array} \right. = \left[ \begin{array}{c} 2\\ -3 \\ 0 \end{array} \right.\)
\(\overrightarrow{AC} = \overrightarrow{OC} - \overrightarrow{OA} = \left[ \begin{array}{c} -1 \\ -2 \\ 5 \end{array} \right. - \left[ \begin{array}{c} 1 \\ 7 \\ 1 \end{array} \right. = \left[ \begin{array}{c} -2\\ -9 \\ 4 \end{array} \right.\)
\(\overrightarrow{AM} = \overrightarrow{OM} - \overrightarrow{OA} = \left[ \begin{array}{c} x \\ y \\ z \end{array} \right. - \left[ \begin{array}{c} 1 \\ 7 \\ 1 \end{array} \right. = \left[ \begin{array}{c} x-1\\ y-7 \\ z-1 \end{array} \right.\)
Calcul de \(\overrightarrow{AB} \wedge \overrightarrow{AC} = \left[ \begin{array}{c} 2 \\ -3 \\ 0 \end{array} \right. \wedge \left[ \begin{array}{c} -2 \\ -9 \\ 4 \end{array} \right. = \left[ \begin{array}{c} -12\\ -8 \\ -24 \end{array} \right.\)
et
\(\begin{array}{ll}\Big(\overrightarrow{AB} \wedge \overrightarrow{AC} \Big) \cdot \overrightarrow{AM} &= \left[ \begin{array}{c} -12 \\ -8 \\ -24 \end{array} \right. \cdot \left[ \begin{array}{c} x-1 \\ y-7 \\ z-1 \end{array} \right. \\ & = -12(x-1) - 8(y-7) - 24(z-1) = 0 \\ & = -12 x + 12 - 8y + 56 - 24z + 24 = 0 \\ & = -12 x - 8y - 24z + 92 = 0 \end{array}\)
après simplification, l'équation du plan est :
\(3x + 2y + 6z - 23 = 0\)
En Physique
Moment d'une force, par rapport à un axe \((\Delta)\) :
Exemple :
\(m_{\Delta} = \Big(\overrightarrow{OM} \wedge \overrightarrow{F} \Big) \cdot \overrightarrow{u}\)
Moment d'une force \(\overrightarrow{F}\) par rapport à un axe \((\Delta)\):
Soit un axe \((\Delta)\) de vecteur unitaire \(\overrightarrow{u}\) et une force \(\overrightarrow{F}\) appliquée au point matériel \(M\).
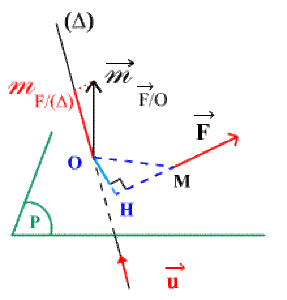
Le moment de \(\overrightarrow{F}\) par rapport au point \(O\) est le vecteur :\( \overrightarrow{m}_{\overrightarrow{F}/o} = \overrightarrow{OM} \wedge \overrightarrow{F}\)
de direction perpendiculaire au plan \((P)\)
de sens : \(\Big(\overrightarrow{OM},\overrightarrow{F},\overrightarrow{m}_{\overrightarrow{F}/o} \Big)\) direct
de module :\(\Big\Arrowvert\overrightarrow{OM}\Big\Arrowvert ~\Big\Arrowvert \overrightarrow{F}\Big\Arrowvert ~\Big\arrowvert \sin\Big(\overrightarrow{OM},\overrightarrow{F}\Big)\Big\arrowvert =\Big\Arrowvert \overrightarrow{F}\Big\Arrowvert~\Big\Arrowvert \overrightarrow{OH}\Big\Arrowvert\)
Le moment de \(\overrightarrow{F}\) par rapport à l'axe \((\Delta)\) est égal à
\(m_{\overrightarrow{F}/(\Delta)} = \overrightarrow{m}_{\overrightarrow{F}/o} \cdot \overrightarrow{u}\) c.à.d. au produit mixte :
\(m_{\overrightarrow{F}/(\Delta)} = \Big( \overrightarrow{OM} \wedge \overrightarrow{F} \Big) \cdot \overrightarrow{u} \quad \forall O \in (\Delta )\)
Pour \(O' \in (\Delta)\) différent de \(O\) : \(\overrightarrow{OM} = \overrightarrow{OO'} + \overrightarrow{O'M}\)
\(\begin{array}{ll}m_{\overrightarrow{F}/(\Delta)} &= \Big( \overrightarrow{OO'} \wedge \overrightarrow{F} \Big) \cdot \overrightarrow{u} + \Big( \overrightarrow{O'M} \wedge \overrightarrow{F} \Big) \cdot \overrightarrow{u} \\ &= \Big( \overrightarrow{O'M} \wedge \overrightarrow{F} \Big) \cdot \overrightarrow{u} \end{array}\)
\(\textrm{ car } \Big( \overrightarrow{OO'} \wedge \overrightarrow{F} \Big) \cdot \overrightarrow{u} = 0 ~\Big( \overrightarrow{OO'} \textrm{ colin\'eaire \`a} \overrightarrow{u}\Big)\)
\(\qquad\)
Moment cinétique d'un point matériel, par rapport à un axe \((\Delta)\) : \(L_{\Delta} = \Big(\overrightarrow{OM} \wedge m\overrightarrow{v} \Big) \cdot \overrightarrow{u}\)
Travail des forces magnétiques :
Exemple :
\(dW = I\Big(\overrightarrow{dl} \wedge \overrightarrow{B} \Big) \cdot \overrightarrow{MM'}\)
Travail des forces magnétiques:
Un élément \(\overrightarrow{dl}\) d'un circuit \((C)\) parcouru par un courant \(I\), placé dans un champ magnétique \(\overrightarrow{B}\) subit la force élémentaire (force de Laplace) :
\(\overrightarrow{dF} = I \overrightarrow{dl} \wedge \overrightarrow{B}\)
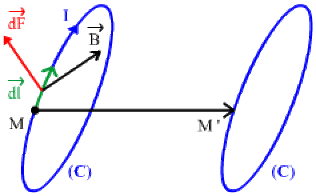
Pour un déplacement \(\overrightarrow{MM'}\) du circuit, le travail des forces magnétiques s'écrit :
\(dW = \overrightarrow{dF} \cdot \overrightarrow{MM'}\)
\(dW = \Big(I\overrightarrow{dl} \wedge \overrightarrow{B} \Big) \cdot \overrightarrow{MM'}\)
\(dW = I\Big(\overrightarrow{dl},\overrightarrow{B},\overrightarrow{MM'} \Big)\)