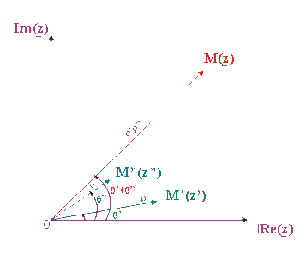Multiplication
Multiplication "algébrique"
\(\underline{z}=\underline{z}'\underline{z}'' \Leftrightarrow a+jb=(a'+jb')(a''+jb'')=(a'a''-b'b'')+j(a'b''+b'a'')\Leftrightarrow \left\{\begin{array}{ll} a= a'a'' - b'b'' \\ b= a'b'' + b'a'' \end{array}\right.\)
Multiplication "polaire"
\(\begin{array}{ll}\underline{z} = \underline{z}' \underline{z}'' \Leftrightarrow \rho(\cos \theta + j \sin \theta) & = \rho'(\cos \theta ' + j \sin \theta') ~\rho''(\cos \theta'' + j \sin \theta'') \\ & =\rho'\rho''\left[\left(\cos \theta'\cos\theta''-\sin\theta'\sin\theta''\right)\right. + \\ & \left.j \left(\sin \theta'\cos\theta''+\cos\theta'\sin\theta''\right)\right] \\ & = \rho' \rho''\left[\cos(\theta' + \theta'') + j \sin(\theta' + \theta'')\right]\end{array}\)
soit \(\rho e^{j \theta} = \rho' e^{j \theta'} \rho'' e^{j \theta''} = \rho' \rho'' e^{j(\theta'+\theta'')}\Leftrightarrow \left\{\begin{array}{ll} \rho = \rho' \rho'' \\ \theta = \theta' + \theta'' \end{array}\right.\)
Multiplication "vecteur-image"
A la vue du résultat de la forme polaire, multiplier le nombre \(\underline{z}'\), de vecteur-image \(\overrightarrow{OM'}\) par un nombre complexe \(\underline{z}''\) de module \(\rho''\) et d'argument \(\theta''\) revient à effectuer sur le "vecteur-image" une rotation d'angle \(+ \theta''\) et une multiplication de son module par \(\rho''\)
\(\underline{z} = \underline{z}' \underline{z}'' \Leftrightarrow \left\{\begin{array}{ll} \underline{z}' \textrm{ de vecteur -image }\overrightarrow{OM'}(\rho',\theta') \\ \underline{z}'' \textrm{ de vecteur -image } \overrightarrow{OM''}(\rho'',\theta'') \end{array}\right.\)
\(\underline{z} = \underline{z}'~ \underline{z}'' \textrm{ de vecteur -image } \overrightarrow{OM}( \rho' \rho'', \theta' + \theta'')\)
Conclusion
L'utilisation de la forme polaire est préférable dans le cas de la multiplication de deux nombres complexes :
Multiplication des modules
Addition des arguments
Exemple :
Soient les nombres complexes
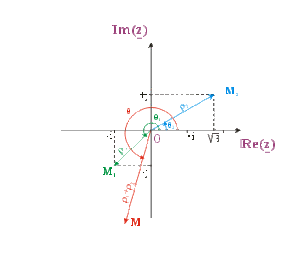
\(\underline{z_{1}} = -1-j\) et \(\underline{z_{2}} =\sqrt{3} +j\) (formes algébriques)
\(\underline{z_{1}} = \sqrt{2} \left[\cos\frac{5 \pi}{4} + j \sin \frac{5 \pi}{4}\right]\)
et \(\underline{z_{2}} = 2 \left[\cos\frac{\pi}{6} + j \sin \frac{\pi}{6}\right]\) (formes trigonométriques)
Multiplication "algébrique":
\(\underline{z}_{1}~\underline{z}_{2} = (-1-j)(\sqrt{3}+j) = 1- \sqrt{3}-j (1+\sqrt{3})\)
Multiplication "polaire":
\(\begin{array}{ll}\underline{Z}_{1}~\underline{Z}_{2} &= \sqrt{2}\left[\cos\frac{5 \pi}{4} + j \sin \frac{5 \pi}{4}\right]2\left[\cos\frac{\pi}{6} + j \sin \frac{\pi}{6}\right] \\ &= 2 \sqrt{2}\left[\cos\left(\frac{5\pi}{4} + \frac{\pi}{6}\right)+j\sin \left(\frac{5 \pi}{4} + \frac{\pi}{6}\right)\right] \end{array}\)
\(\underline{Z}_{1}~\underline{Z}_{2} = 2 \sqrt{2} \left[\cos \frac{17 \pi}{12} + j \sin \frac{17 \pi}{12}\right]\)
Multiplication "vectorielle":