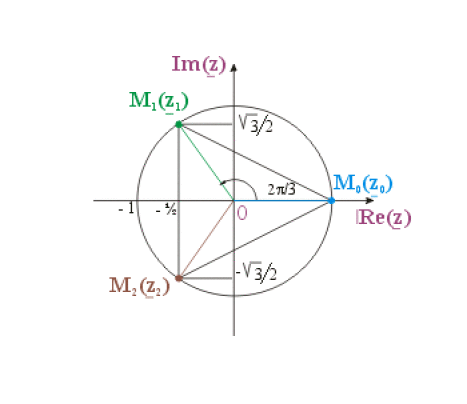Racine n-ième -Définition
On appelle racine n-ième d'un nombre complexe \(\underline{Z}\) tout nombre complexe \(\underline{z}\) vérifiant \((\underline{z} )^{n} =\underline{Z}\). De nouveau l'utilisation de la forme polaire nous amène à poser \(\underline{z} = \rho e^{j\theta}\) et \(\underline{Z} = R e^{j\phi}\) d'où :
\(\left(\underline{z}\right )^{n} = \underline{Z} \Leftrightarrow \left(\rho e^{j \theta}\right)^{n} = \rho^{n}e^{j n \theta} = R e^{j \phi}\)
soit par identification
Donc, \(\underline{Z}\) admet \(n\) racines n-ièmes, qui sont les nombres complexes :
\(\underline{z}_{k} = \sqrt[n]{R}~e^{j\left(\frac{\phi}{n}+\frac{2 k \pi}{n}\right)}\) avec \(k \in \left\{0,1,...n-1\right\}\)
Exemple :
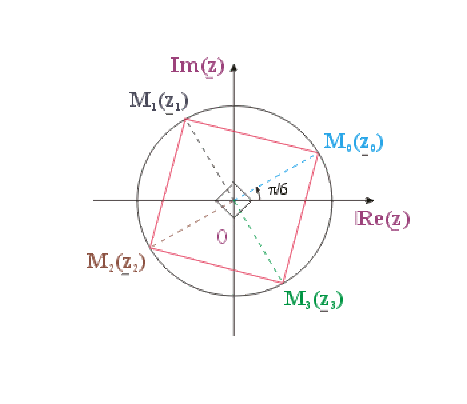
Résoudre \(\underline{z}^{4} = 8 \left(1+j \sqrt{3} \right)\) dans \(\mathbb{C}\)
Soit \(\underline{Z} = 8 (-1 + j \sqrt{3})\) donc \(\left\arrowvert \underline{Z}\right\arrowvert = \left\arrowvert 8 \right\arrowvert \left\arrowvert -1+j\sqrt{3} \right\arrowvert = 8 \sqrt{(-1)^{2} + (\sqrt{3})^{2}} = 16\)
et \(\varphi\) un argument de \(\underline{Z}\) avec \(\cos \varphi = \frac{-8}{16} = \frac{-1}{2}\) et \(\sin \varphi = \frac{8 \sqrt{3}}{16} = \frac{\sqrt{3}}{2}\)
donc \(\cos \varphi = \cos \frac{2 \pi}{3}\) et \(\sin \varphi = \sin \frac{2 \pi}{3} \Rightarrow \varphi = \frac{2 \pi}{3} \left(2 \pi \right)\).
d'où \(\underline{Z} = 16 ~e^{j ~2 \pi/6}\) et les valeurs de \(\underline{z}\) telles que \(\underline{z^{4}} =Z\)sont les racines:
\(\underline{z}_{k} = \sqrt[4]{16}~e^{j\left(\pi/6 + k \pi/2\right)} \quad k \in \{0,1,2,3 \}\)
\(\underline{z}_{k} = 2 ~e^{j\left(\pi/6 + k \pi/2\right)} \quad k \in \{0,1,2,3 \}\)
\(\qquad\)
\(k=0\)
\(\underline{z}_{0} = 2~ e^{j\pi/6} = 2 \left(\frac{\sqrt{3}}{2} + j\frac{1}{2}\right) = \sqrt{3} + j\)
\(k=1\)
\(\underline{z}_{1} = 2 ~e^{j\pi/6} .e^{j\pi/2} = z_{0} ~j = -1 + j \sqrt{3}\)
\(k=2\)
\(\underline{z}_{2} = 2 ~e^{j\pi/6} .e^{j\pi} = z_{1} ~j = -\sqrt{3} - j\)
\(k=3\)
\(\underline{z}_{3} = 2 ~e^{j\pi/6} ~.~e^{j3\pi/2} = z_{2} ~j = 1 - j \sqrt{3}\)
On appelle racine n-ième d'un nombre complexe \(\underline{Z} = 1\) tout nombre complexe \(\underline{z}\) vérifiant \(( \underline{z} )^{n} = \underline{1}\)
En posant : \(1=e^{j 2 k \pi}\) et \(\underline{z} = \rho e^{j \theta}\)
Nous obtenons : \(\left(\underline{z}\right)^{n} = 1 \Leftrightarrow (\rho e^{j \theta})^{n} = \rho^{n} e^{j n \theta} = 1 = e^{j 2 k \pi}\)
Soit par identification : \(\left\{\begin{array}{ll} \rho^{n} = 1 \Leftrightarrow \rho = 1 \\ n \theta = 2 k \pi \Leftrightarrow \theta = \frac{2 k \pi}{n} \end{array}\right.\)
D'où les racines -n-ièmes de l'unité sont les nombres complexes:
\(\underline{z}_{k} = e^{j 2k\pi/n}\) avec \(k \in \{0,1,...,n-1\}\)
Exemple :
Racine cubique de l'unité \(\underline{Z}=1\)
On veut résoudre \(\underline{Z}^{3} = Z\) avec \(\underline{Z}=1\)
en posant : \(\underline{z} = \rho ~e^{j \theta}\) et \(\underline{Z} = 1 ~e^{j ~2 k \pi}\)
nous obtenons :
\(\underline{z}^{3} = \underline{Z} \Rightarrow \rho^{3}~e^{j 3 \theta} = 1~e^{j 2k \pi} \Leftrightarrow \left\{\begin{array}{ll} \rho^{3} = 1 \Leftrightarrow \rho = 1 \\ 3 \theta = 2 k \pi \Leftrightarrow \theta = \frac{2 k \pi}{3} ~k\in\{0,1,2\}\end{array}\right.\)
d'où :
\(\underline{z}_{k} = 1 ~e^{j2k\pi/3}~k\in \{0,1,2\}\)
\(\qquad\)
\(k=0\quad \underline{z}_{0} = e^{j 0} = 1\)
\(k=1 \quad \underline{z}_{1} = e^{j 2 \pi/3} = - \frac{1}{2} + j \frac{\sqrt{3}}{2}\)
\(k=2 \quad \underline{z}_{2} = e^{j 4 \pi/3} = - \frac{1}{2} - j \frac{\sqrt{3}}{2}\)